
【题目】如图,四棱锥![]() 中,
中, ![]() 为等边三角形,且平面
为等边三角形,且平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
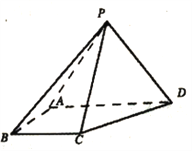
(Ⅰ)证明: ![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() ,结合条件可证得
,结合条件可证得![]() 平面
平面![]() ,于是
,于是![]() ,又
,又![]() ,故可得
,故可得![]() .(Ⅱ)由题意可证得
.(Ⅱ)由题意可证得![]() ,
, ![]() ,
, ![]() 两两垂直,建立空间直角坐标系,通过求出平面
两两垂直,建立空间直角坐标系,通过求出平面![]() 和平面
和平面![]() 的法向量可求解本题.
的法向量可求解本题.
试题解析:
证明:(Ⅰ)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
在底面![]() 中,可得四边形
中,可得四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .
.
(Ⅱ)∵平面![]() 面
面![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
由此可得![]() ,
, ![]() ,
, ![]() 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系![]() .
.
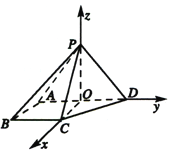
∵直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,即
,即![]() ,
,
由![]() ,知
,知![]() ,得
,得![]() .
.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() .
.
由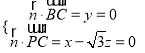 ,得
,得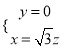 .
.
令![]() ,则
,则![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由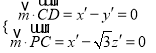 ,得
,得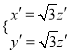 .
.
令![]() ,则
,则![]() ,
,
∴![]()
![]()
![]() ,
,
由图形知二面角![]() 为钝角,
为钝角,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】设函数f (x)=ln x-x+1.
(1)讨论函数f (x)的单调性;
(2)证明当x∈(1,+∞)时, ![]() ;
;
(3)设c>1,证明当x∈(0,1)时,1+(c-1)x>cx.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某亲子游戏结束时有一项抽奖活动,抽奖规则是:盒子里面共有5个小球,小球上分别写有0,1,2,3,4的数字,小球除数字外其它完全相同,每对亲子中,家长先从盒子中取出一个小球,记下数字后将小球放回,孩子再从盒子中取出一个小球,记下小球上数字将小球放回.抽奖活动的奖励规则是:①若取出的两个小球上数字之积大于8,则奖励飞机玩具一个;②若取出的两个小球上数字之积在区间![]() 上,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于2,则奖励饮料一瓶.
上,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于2,则奖励饮料一瓶.
(1)求每对亲子获得飞机玩具的概率;
(2)试比较每对亲子获得汽车玩具与获得饮料的概率,哪个更大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.

(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,其左焦点与抛物线
,其左焦点与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程;
的方程;
(2)过动点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,
,![]() 在第一象限,
在第一象限,![]() ,过点
,过点![]() 做
做![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于点
于点![]() ,连接
,连接![]() 并延长交椭圆
并延长交椭圆![]() 于另一点
于另一点![]() .设直线
.设直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明:![]() 为定值.
为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.
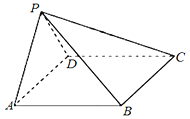
(1).证明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱锥PABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com