练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    数列1，1，2，1，1，2，3，2，1，1，2，3，4，3，2，1，…，则第100项为（　　）
    A、1B、2C、3D、4
    考点：数列的概念及简单表示法
    专题：点列、递归数列与数学归纳法
    分析：将数列的项重新分组，得到数列项的规律，即可得到结论．
    解答： 解：将数列的数进行重新分组，1，（1，2，1），（1，2，3，2，1），（1，2，3，4，3，2，1），…，
    则每组的个数分别为1，3，5，7，…，
    则设第100项位于第n组，则n+
    n(n-1)
    2
    ×2    =n2，由n2=100，
    解得n=10，即第100项是第10组的最后一个数，为1，
    故选：A．
    点评：本题主要考查数列的概念，根据数列特点，寻找规律是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    一只艘船以均匀的速度由A点向正北方向航行，如图，开始航行时，从A点观测灯塔C的方位角（从正北方向顺时针转到目标方向的水平角）为45°，行驶60海里后，船在B点观测灯塔C的方位角为75°，则A到C的距离是（　　）海里．
    A、30（
    		6
    +
    		2
    ）
    B、30（
    		6
    -
    		2
    ）
    C、30（
    		6
    -
    		3
    ）
    D、30（
    		6
    +
    		3
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线
    x2
    a2
    -
    y2
    b2
    =1(b＞a＞0)    的两条渐近线为l1，l2，过右焦点F作垂直l1的直线交l1，l2于A，B两点．若|OA|，|AB|，|OB|成等差数列，则双曲线的离心率为（　　）
    A、
    		5
    2
    B、
    		5
    C、
    		3
    D、
    		3
    +1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

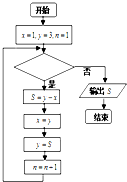    已知数列{an}满足a1=1，a2=3，an+2=an+1-an，n∈N*，利用如图所示的程序框图计算该数列的第n项（n≥3），若输出S的结果为1，则判断框内的条件可能是（　　）
    A、n≤5？B、n≤6？
    C、n≤7？D、n≤8？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=x2-ax+2在（2，+∞）上单调递增，则a的取值范围为（　　）
    A、[2，+∞）
    B、[4，+∞）
    C、（-∞，4]
    D、（-∞，-4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面几个推理过程是演绎推理的是（　　）
    A、某同学第一次数学考试65分，第二次考试68分，由此预测其第三次考试71分
    B、根据圆的面积为S=πr2，推测球的体积为V=πr3
    C、在数列{an}中，根据a1=1，an+1=
    an
    an+1
    ，n∈N*，计算出a2，a3，a4的值，然后猜想{an}的通项公式
    D、因为平行四边形的对角线互相平分，而菱形是平行四边形，所以菱形的对角线互相平分

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    “x=2”是“log2|x|=1”的（　　）
    A、充分不必要条件
    B、必要不充分条件
    C、充分必要条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知等比数列{an}满足a3-a1=3，a1+a2=3．
    （Ⅰ）求数列{an}的前15项的和S15；
    （Ⅱ）若等差数列{bn}满足b1=a2，b3=a2+a3，求数列{bn}的前n项的和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

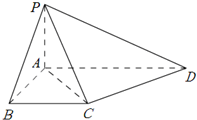    如图，在四棱锥P-ABCD，PA⊥平面ABCD，PA=AB=BC=
    1
    2
    AD，四边形ABCD是直角梯形中，∠ABC=∠BAD=90°．
    （1）求证：CD⊥平面PAC；
    （2）求二面角A-PD-C的余弦值．

    查看答案和解析>>

    同步练习册答案