
分析 令a=b=0,a=b=1,可得f(0),f(1),可判断①;令a=b=-1,求得f(-1),再由奇偶性的定义,可判断②;
再由f(2)=2,运用已知等式,求得f(2n)=f(2•2n-1)=2f(2n-1)+2n=…=n•2n,可得数列{an}、数列{bn}的通项公式,即可判断③④.
解答 解:∵取a=b=0,可得f(0)=0,
取a=b=1,可得f(1)=2f(1),即f(1)=0,
∴f(0)=f(1),
即①正确;
令a=b=-1,则f(1)=-f(-1)-f(-1)=0⇒f(-1)=0,
令a=-1,则f(-b)=-f(b)+bf(-1)=-f(b)⇒f(x)为奇函数,
即②正确;
∵f(ab)=af(b)+bf(a),
∴f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)
=2f(2n-1)+2n=…=n•2n,
∴an=$\frac{f({2}^{n})}{{2}^{n}}$=n,bn=$\frac{f({2}^{n})}{n}$=2n,
即有③④正确.
故答案为:①②③④.
点评 本题考查抽象函数的函数值的求法,注意运用赋值法,考查函数的奇偶性的判断,注意运用定义法,同时考查等差数列和等比数列的判定,注意运用运用通项公式,考查推理能力和运算能力,属于中档题和易错题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:解答题
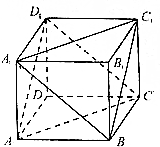 已知正方体ABCD-A1B1C1D1的棱长为a.
已知正方体ABCD-A1B1C1D1的棱长为a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3•({1-{3^n}})}}{1-3}$ | B. | $\frac{{3•({1-{3^{2n+1}}})}}{1-3}$ | C. | $\frac{{3•({1-{9^n}})}}{1-9}$ | D. | $\frac{{3•({1-{9^{n+1}}})}}{1-9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| X | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{4}$ | m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 0 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
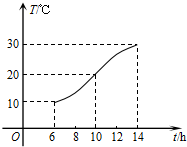 某地一天中6时至14时的温度变化曲线近似满足函数T=Asin(ωt+φ)+b(其中$\frac{π}{2}$<φ<π),6时至14时期间的温度变化曲线如图所示,它是上述函数的半个周期的图象,那么这一天6时至14时温差的最大值是20°C;图中曲线对应的函数解析式是y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
某地一天中6时至14时的温度变化曲线近似满足函数T=Asin(ωt+φ)+b(其中$\frac{π}{2}$<φ<π),6时至14时期间的温度变化曲线如图所示,它是上述函数的半个周期的图象,那么这一天6时至14时温差的最大值是20°C;图中曲线对应的函数解析式是y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com