
分析 (I)利用线段的垂直平分线的性质、椭圆的定义即可得出.
( II)当直线l不垂直于x轴时,设直线l方程为y=kx+m,P(x1,y1),Q(x2,y2),由于OP⊥OQ,可得$\overrightarrow{OP}•\overrightarrow{OQ}=0$,即x1x2+y1y2=0,直线方程与椭圆方程联立可得(3+4k2)x2+8kmx+4m2-12=0,△>0,由x1x2+y1y2=0,利用根与系数的关系可得:${m^2}=\frac{{12+12{k^2}}}{7}$,代入△>0成立,原点O到直线l的距离可得:d=$\sqrt{\frac{12}{7}}$,直线y=kx+m与圆${x^2}+{y^2}=\frac{12}{7}$相切. 当直线l垂直于x轴时也成立.
解答 解:(Ⅰ)∵点N在线段MB的垂直平分线上,∴|NB|=|NM|,
∴|NA|+|NB|=|NA|+|NM|=|AM|=4>|AB|,
∴点N的轨迹是以A,B为焦点,长轴长为4的椭圆.
设此椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,则$\left\{{\begin{array}{l}{2a=4}\\{{a^2}-{b^2}=1}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{a=2}\\{b=\sqrt{3}}\end{array}}\right.$,
∴曲线C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
( II)当直线l不垂直于x轴时,设直线l方程为y=kx+m,P(x1,y1),Q(x2,y2),
∵OP⊥OQ,∴$\overrightarrow{OP}•\overrightarrow{OQ}=0$,即x1x2+y1y2=0,
由$\left\{{\begin{array}{l}{\frac{x^2}{4}+\frac{y^2}{3}=1}\\{y=kx+m}\end{array}}\right.$得(3+4k2)x2+8kmx+4m2-12=0,
∴△=64k2m2-4(3+4k2)(4m2-12)>0,…(*)
${x_1}+{x_2}=-\frac{8km}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{4{m^2}-12}}{{3+4{k^2}}}$.
则${x_1}{x_2}+{y_1}{y_2}={x_1}{x_2}+(k{x_1}+m)(k{x_2}+m)=(1+{k^2}){x_1}{x_2}+km({x_1}+{x_2})+{m^2}$=$(1+{k^2})×\frac{{4{m^2}-12}}{{3+4{k^2}}}+km×(-\frac{8km}{{3+4{k^2}}})+{m^2}=0$,
解得${m^2}=\frac{{12+12{k^2}}}{7}$,代入可知不等式(*)成立,
∴原点O到直线l的距离为$d=\frac{|m|}{{\sqrt{{k^2}+1}}}=\frac{{\sqrt{\frac{{12+12{k^2}}}{7}}}}{{\sqrt{{k^2}+1}}}=\sqrt{\frac{12}{7}}$,
∴直线y=kx+m与圆${x^2}+{y^2}=\frac{12}{7}$相切.
当直线l垂直于x轴时,不妨设点P在x轴上方,
根据椭圆的对称性,易得直线OP的方程为y=±x,
由$\left\{{\begin{array}{l}{\frac{x^2}{4}+\frac{y^2}{3}=1}\\{y=±x}\end{array}}\right.$,解得$P(±\sqrt{\frac{12}{7}}\;,\;\sqrt{\frac{12}{7}})$,
∴原点O到直线l距离为$\sqrt{\frac{12}{7}}$,因此直线l与圆${x^2}+{y^2}=\frac{12}{7}$相切.
综上所述:存在定圆${x^2}+{y^2}=\frac{12}{7}$,使得该圆恒与直线l相切.
点评 本题考查了椭圆的标准方程及其性质、直线与圆相切的充要条件、点到直线的距离公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
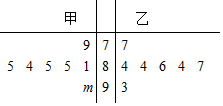 如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )
如图是七位评委为甲、乙两名比赛歌手打出的分数的茎叶图(其中m为数字0-9中的一个),甲、乙两名选手得分的平均数分别为a1,a2,若a1=a2,则m=( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 1 | 2 | 4 | 5 |
| 销售额y(万元) | 6 | 14 | 28 | 32 |
| A. | 66.2万元 | B. | 66.4万元 | C. | 66.8万元 | D. | 67.6万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B={1,2,3} | B. | A=B | C. | A∩B={1,2,3} | D. | B⊆A |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com