
设 和
和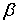 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于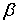 内的两条直线,
内的两条直线,
则 平行于
平行于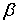 ;
;
(2)若 外一条直线
外一条直线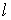 与
与 内的一条直线平行,则
内的一条直线平行,则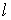 和
和 平行;
平行;
(3)设 和
和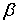 相交于直线
相交于直线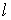 ,若
,若 内有一条直线垂直于
内有一条直线垂直于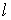 ,则
,则 和
和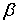 垂直;
垂直;
(4)直线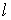 与
与 垂直的充分必要条件是
垂直的充分必要条件是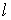 与
与 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
如图,过点 的两直线与抛物线
的两直线与抛物线 相切于A、B两点, AD、BC垂直于直线
相切于A、B两点, AD、BC垂直于直线 ,垂足分别为D、C.
,垂足分别为D、C.
(1)若 ,求矩形ABCD面积;
,求矩形ABCD面积;
(2)若 ,求矩形ABCD面积的最大值.
,求矩形ABCD面积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
(1)在学习函数的奇偶性时我们知道:若函数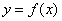 的图像关于点
的图像关于点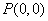 成中心对称图形,则有函数
成中心对称图形,则有函数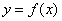 为奇函数,反之亦然;现若有函数
为奇函数,反之亦然;现若有函数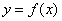 的图像关于点
的图像关于点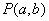 成中心对称图形,则有与
成中心对称图形,则有与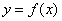 相关的哪个函数为奇函数,反之亦然.
相关的哪个函数为奇函数,反之亦然.
(2)将函数 的图像向右平移2个单位,再向下平移16个单位,求此时图像对应的函数解释式,并利用(1)的性质求函数
的图像向右平移2个单位,再向下平移16个单位,求此时图像对应的函数解释式,并利用(1)的性质求函数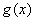 图像对称中心的坐标;
图像对称中心的坐标;
(3)利用(1)中的性质求函数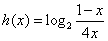 图像对称中心的坐标,并说明理由.
图像对称中心的坐标,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定点A(-2, 0)和B(2, 0),曲线E上任一点P满足|PA|-|PB|=2.
(1)求曲线E的方程;
(2)延长PB与曲线E交于另一点Q,求|PQ|的最小值;
(3)若直线l的方程为x=a(a≤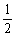 ),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。
),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com