
已知定点A(-2, 0)和B(2, 0),曲线E上任一点P满足|PA|-|PB|=2.
(1)求曲线E的方程;
(2)延长PB与曲线E交于另一点Q,求|PQ|的最小值;
(3)若直线l的方程为x=a(a≤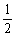 ),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。
),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。
解:(1)由双曲线的定义得:曲线E是以A,B为焦点的双曲线的右支,所以曲线E的方程为:x2-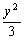 =1(x>0)
=1(x>0)
(2)若直线PQ不垂直于x轴,设直线PQ的方程为:y=k(x-2)
由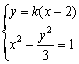 ,得(3-k2)x2+4k2x-(4k2+3)=0
,得(3-k2)x2+4k2x-(4k2+3)=0
设p(x1,y1),Q(x2,y2),这里x1>0,x2>0
则: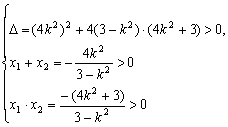 得:k2>3
得:k2>3
|PQ|=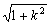 |x1-x2|=
|x1-x2|=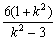 =6+
=6+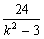 >6
>6
若直线PQ垂直于x轴,则直线PQ的方程为x=2。
这时P(2,3),Q(2,-3),所以|PQ|=6,
综上:|PQ|min=6 ……………………………9分
(3)据题意得:|CR|=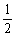 |PQ|。若直线PQ不垂直于x轴,
|PQ|。若直线PQ不垂直于x轴,
由|CR|=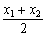 -a=
-a= -a
-a
∴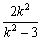 -a=
-a=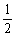 ·
·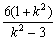 ,a=
,a=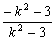 =-1+
=-1+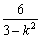 <-1
<-1
若直线PQ垂直于x轴,这时|PQ|=6,|CR|=2-a
∴a=-1。
综上a≤-1。


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
设 和
和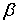 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若 内的两条相交直线分别平行于
内的两条相交直线分别平行于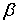 内的两条直线,
内的两条直线,
则 平行于
平行于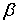 ;
;
(2)若 外一条直线
外一条直线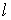 与
与 内的一条直线平行,则
内的一条直线平行,则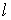 和
和 平行;
平行;
(3)设 和
和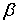 相交于直线
相交于直线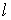 ,若
,若 内有一条直线垂直于
内有一条直线垂直于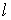 ,则
,则 和
和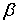 垂直;
垂直;
(4)直线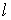 与
与 垂直的充分必要条件是
垂直的充分必要条件是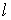 与
与 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l1: 4x-3y+6=0和直线l2: x=-1,抛物线y2=4x上一动点P,P到直线l1和直线l2的距离之和的最小值是
A.2 B.3 C.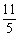 D.
D.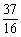
查看答案和解析>>
科目:高中数学 来源: 题型:
设集合A=(―∞, ―2]∪[3, +∞),关于x的不等式(x-2a)·(x+a)>0的解集为B(其中a<0).
(1)求集合B;
(2)设p: x∈A, q: x∈B,且Øp是Øq的充分不必要条件,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,程序框图输出的所有实数对(x, y)所对应的点都在函数
A.y=x+1的图象上 B.y=2x的图象上 C.y=2x的图象上 D.y=2x-1的图象上
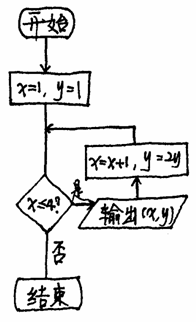
查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的函数f(x)在(6, +∞)上为减函数,且函数y=f(x+6)为偶函数,则
A.f(4)>f(5) B.f(4)>f(7) C.f(5)>f(7) D.f(5)>f(8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com