
点P(sin2014°,tan2014°)位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
2010年7月1日某人到银行存入一年期款a元,若年利率为x,按复利计算,则到2015年7月1日可取款( )
A.a(1+x)5元 B.a(1+x)6元
C.a+(1+x)5元 D.a(1+x5)元
查看答案和解析>>
科目:高中数学 来源: 题型:
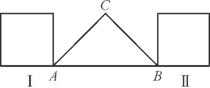
如图,在△ABC中,∠C=90°,AC=BC=2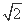 ,一个边长2的正方形由位置Ⅰ沿边AB平行移动到位置Ⅱ,若移动的距离为x,正方形和三角形的公共部分的面积为f(x).
,一个边长2的正方形由位置Ⅰ沿边AB平行移动到位置Ⅱ,若移动的距离为x,正方形和三角形的公共部分的面积为f(x).
(1) 求f(x)的解析式;
(2) 在坐标系中画出函数y=f(x)的草图;
(3) 根据图象,指出函数y=f(x)的单调区间和最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知点P(sinα-cosα,tanα)在第一象限,则在[0,2π]内,α的取值范围是( )
A.(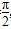 ,
,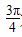 )∪(π,
)∪(π,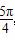 ) B.(
) B.( ,
,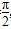 )∪(π,
)∪(π,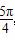 )
)
C.(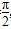 ,
,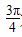 )∪(
)∪(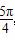 ,
, ) D.(
) D.( ,
,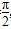 )∪(
)∪(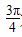 ,π)
,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知α为锐角,且2tan(π-α)-3cos( +β)+5=0,tan(π+α)+6sin(π+β)=1,则sinα的值是( )
+β)+5=0,tan(π+α)+6sin(π+β)=1,则sinα的值是( )
A.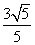 B.
B.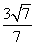
C. D.
D.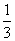
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,a、b、c分别是角A、B、C的对边,向量m=(b,2a-c),n=(cosB,cosC),且m∥n.
(1)求角B的大小;
(2)设f(x)=cos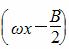 +sinωx(ω>0),且f(x)的最小正周期为π,求f(x)在区间[0,
+sinωx(ω>0),且f(x)的最小正周期为π,求f(x)在区间[0, ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com