
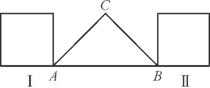
如图,在△ABC中,∠C=90°,AC=BC=2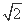 ,一个边长2的正方形由位置Ⅰ沿边AB平行移动到位置Ⅱ,若移动的距离为x,正方形和三角形的公共部分的面积为f(x).
,一个边长2的正方形由位置Ⅰ沿边AB平行移动到位置Ⅱ,若移动的距离为x,正方形和三角形的公共部分的面积为f(x).
(1) 求f(x)的解析式;
(2) 在坐标系中画出函数y=f(x)的草图;
(3) 根据图象,指出函数y=f(x)的单调区间和最大值.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
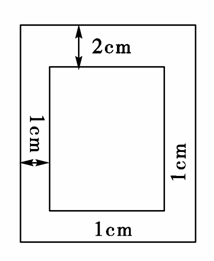
如图,书的一页的面积为600cm2,设计要求书面上方空出2cm的边,下、左、右方都空出1cm的边,为使中间文字部分的面积最大,这页书的长、宽应分别为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
直线y=2x+1和圆x2+y2=1交于A、B两点,以x轴的正方向为始边,OA为终边(O是坐标原点)的角为α,OB为终边的角为β,则sin(α+β)的值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=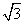 sin
sin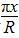 图象上相邻的一个最大值点与一个最小值点恰好都在圆x2+y2=R2上,则f(x)的最小正周期为( )
图象上相邻的一个最大值点与一个最小值点恰好都在圆x2+y2=R2上,则f(x)的最小正周期为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com