方程x2＋ax－2＝0在区间[1,5]上有解，则实数a的取值范围为( )
A．(－
，＋∞) B．(1，＋∞)
C．[－，1] D．(－∞，－)
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案科目：高中数学 来源： 题型：
已知函数f(x)＝logax在[2，＋∞)上恒有|f(x)|>1，则( )
A．0<a<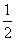
或1<a<2 B．0<a<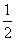或a>2
C.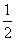<a<1或1<a<2 D.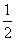<a<1或a>2
查看答案和解析>>
科目：高中数学 来源： 题型：
我们定义若函数f(x)为D上的凹函数须满足以下两条规则：(1)函数在区间D上的任何取值有意义；(2)对于区间D上的任意n个值x1，x2，…，xn，总满足f(x1)＋f(x2)＋…＋f(xn)≥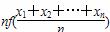
，那么下列四个图像中在[0，
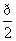]上满足凹函数定义的是( )
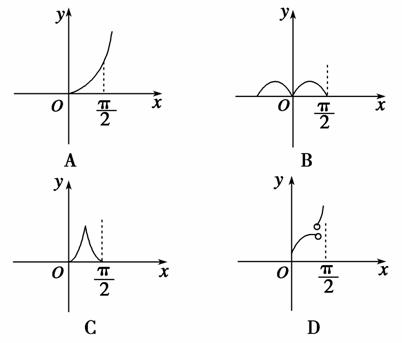
查看答案和解析>>
科目：高中数学 来源： 题型：
如果函数f(x)＝x2＋bx＋c对任意的实数x都有f(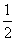
＋x)＝f(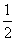－x)，那么( )
A．f(－2)<f(0)<f(2) B．f(0)<f(－2)<f(2)
C．f(2)<f(0)<f(－2) D．f(0)<f(2)<f(－2)
查看答案和解析>>
科目：高中数学 来源： 题型：
已知函数f(x)＝x2－2(a＋2)x＋a2，g(x)＝－x2＋2(a－2)x－a2＋8，设H1(x)＝max{f(x)，g(x)}，H2(x)＝min{f(x)，g(x)}(max{p，q}表示p，q中的较大值，min{p，q}表示p，q中的较小值)．记H1(x)的最小值为A，H2(x)的最大值为B，则A－B＝( )
A．16 B．－16
C．a2－2a－16 D．a2＋2a－16
查看答案和解析>>
科目：高中数学 来源： 题型：
若a<b<c，则函数f(x)＝(x－a)(x－b)＋(x－b)(x－c)＋(x－c)(x－a)的两个零点分别位于区间( )
A．(a，b)和(b，c)内
B．(－∞，a)和(a，b)内
C．(b，c)和(c，＋∞)内
D．(－∞，a)和(c，＋∞)内
查看答案和解析>>
科目：高中数学 来源： 题型：
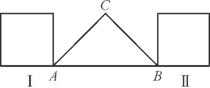
如图,在△ABC中,∠C=90°,AC=BC=2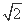
,一个边长2的正方形由位置Ⅰ沿边AB平行移动到位置Ⅱ,若移动的距离为x,正方形和三角形的公共部分的面积为f(x).
(1) 求f(x)的解析式;
(2) 在坐标系中画出函数y=f(x)的草图;
(3) 根据图象,指出函数y=f(x)的单调区间和最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则使函数f(x)的图像位于直线y＝1上方的x的取值范围是________．