用“辗转相除法求得360和504的最大公约数是( )A．36B．72C．24D．2 520 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

14．用“辗转相除法”求得360和504的最大公约数是（　　）

A．

B．

C．

D．

2 520

分析用较大的数字除以较小的数字，得到商和余数，然后再用上一式中的除数和得到的余数中较大的除以较小的，以此类推，当整除时，就得到要求的最大公约数．

解答解：∵504÷360=1…144
360÷144=2…72
144÷72=2
∴360和504的最大公约数是72
故选A．

点评本题考查用辗转相除法求两个数的最大公约数，本题是一个基础题，在解题时注意数字的运算不要出错，注意与更相减损术进行比较．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

4．设△ABC的内角A，B，C所对边的长分别为a，b，c，则下列命题正确的个数是．（　　）
①若ab＞c²，则$C＜\frac{π}{3}$
②若a+b＞2c，则$C＜\frac{π}{3}$
③若a³+b³=c³，则$C＜\frac{π}{2}$
④若（a+b）c＜2ab，则$C＞\frac{π}{2}$
⑤若（a²+b²）c²＜2a²b²，则$C＞\frac{π}{3}$．

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．一台机器由于使用时间较长，但还可以使用，它按不同的转速生产出来的某机器零件有一些会有缺点，每小时生产有缺点零件的多少随机器运转的速度而变化，如表是抽样试验结果：

转速x/（rad/s）	16	14	12	8
每小时生产有缺点的零件数y/件	11	9	8	5

若实际生产中，允许每小时的产品中有缺点的零件数最多为10个，那么机器的转速应该控制所在的范围是（　　）

A．

10转/s以下

B．

15转/s以下

C．

20转/s以下

D．

25转/s以下

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．已知命题p：“x∈R时，都有x²-x+$\frac{1}{4}$＜0”；命题q：“存在x∈R，使sinx+cosx=$\sqrt{2}$成立”．则下列判断正确的是（　　）

A．

p∨q为假命题

B．

p∧q为真命题

C．

￢p∧q为真命题

D．

￢p∨￢q是假命题

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

9．已知集合M={x|-2≤x≤2}，N={x|y=$\sqrt{1-x}$}，那么M∩N=（　　）

A．

[-2，1]

B．

（-2，1）

C．

（-2，1]

D．

{-2，1}

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

19．

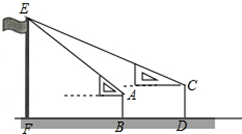某校高一年级某班开展数学活动，小李和小军合作用一副三角板测量学校的旗杆，小李站在B点测得旗杆顶端E点的仰角为45°，小军站在点D测得旗杆顶端E点的仰角为30°，已知小李和小军相距（BD）6米，小李的身高（AB）1.5米，小军的身高（CD）1.75米，求旗杆的高EF的长．（结果精确到0.1，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．

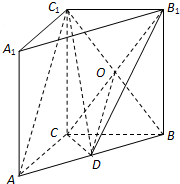（理科做）如图，在直三棱柱ABC-A₁B₁C₁中，AC⊥BC，点D是AB的中点．
求证：
（1）AC⊥BC₁；
（2）AC₁∥平面B₁CD．
（3）若AC=BC=$\frac{1}{2}$CC₁，求直线CC₁与平面ABC₁所成角的正切值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

3．已知函数f（x）=ax^-3+bsinx+x²+8（ab≠0），且f（-2）=3，则f（2）=21．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．

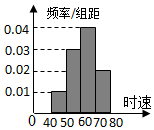关于统计数据的分析，有以下几个结论：
①一组数不可能有两个众数；
②将一组数据中的每个数据都减去同一个数后，方差没有变化；
③调查剧院中观众观看时的感受，从50排（每排人数相同）中任意取一排的人参加调查，属于分层抽样；
④如图是随机抽取的200辆汽车通过某一段公路时的时速分布直方图，根据这个直方图，可以得到时速在[50，60]的汽车大约是60辆．
这4种说法中正确的个数是（　　）

A．

B．

C．

D．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学