
分析 (1)利用同角三角函数关系和已知条件f(α)=-$\frac{3}{26}$求得$\frac{{4\sqrt{3}m}}{13}-\frac{-11}{26}-1=-\frac{3}{26}$,由此得到m的值;则易得函数f(x)=sin(2x-$\frac{π}{6}$)-1,根据正弦函数的性质来求最小正周期;
(2)利用(1)中得到的函数解析式和正弦函数的单调增区间解答.
解答 解:(1)$f(α)=msin2α-\frac{1}{2}cos2α-1=m•\frac{2tanα}{{1+{{tan}^2}α}}-\frac{1}{2}•\frac{{1-{{tan}^2}α}}{{1+{{tan}^2}α}}-1=\frac{{4\sqrt{3}m}}{13}-\frac{-11}{26}-1$,
又∵$f(α)=-\frac{3}{26}$,
∴$\frac{{4\sqrt{3}m}}{13}-\frac{-11}{26}-1=-\frac{3}{26}$,即$m=\frac{{\sqrt{3}}}{2}$;
故$f(x)=\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cos2x-1=sin({2x-\frac{π}{6}})-1$,
∴函数f(x)的最小正周期$T=\frac{2π}{2}=π$;
(2)f(x)的递增区间是$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$,
∴$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3},k∈Z$,所以在[0,π]上的递增区间是[0,$\frac{π}{3}$]∪[$\frac{5π}{6}$,π].
点评 本题主要考查了三角函数中的恒等变换应用,正弦函数的单调性.考查了学生基础知识的综合运用.


科目:高中数学 来源: 题型:解答题
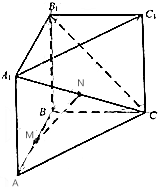 如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB⊥BC,AB=BC=BB1=2,M,N分别是AB,A1C的中点.
如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB⊥BC,AB=BC=BB1=2,M,N分别是AB,A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
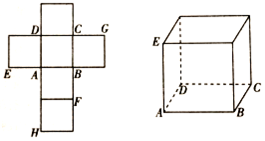 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届山东临沭一中高三上学期10月月考数学(文)试卷(解析版) 题型:解答题
已知数列 是等差数列,
是等差数列, 是等比数列,且
是等比数列,且 ,
, ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)数列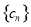 满足
满足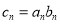 ,求数列
,求数列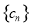 的前
的前 项和
项和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com