
分析 求出$\overrightarrow{OB}$方向上的单位向量$\overrightarrow{e}$,则有点C在∠AOB的平分线上,故存在实数λ使得$\overrightarrow{OC}$=λ($\overrightarrow{OA}$+$\overrightarrow{e}$),如此可以得到坐标的参数表达式,再由|$\overrightarrow{OC}$|=$\sqrt{10}$,建立方程求出参数的值,即可得出点C的坐标.
解答 解:由题意$\overrightarrow{OA}$=(0,-1),是一个单位向量,
由于$\overrightarrow{OB}$=(-3,-4),故$\overrightarrow{OB}$方向上的单位向量$\overrightarrow{e}$=(-$\frac{3}{5}$,-$\frac{4}{5}$),
∵点C在∠AOB的平分线上,∴存在实数λ使得$\overrightarrow{OC}$=λ($\overrightarrow{OA}$+$\overrightarrow{e}$)=λ(-$\frac{3}{5}$,-1-$\frac{4}{5}$)=λ(-$\frac{3}{5}$,-$\frac{9}{5}$),
∵|$\overrightarrow{OC}$|=$\sqrt{10}$,
∴λ2×($\frac{9}{25}$+$\frac{81}{25}$)=10,解得λ=$\frac{5}{3}$,代入得 $\overrightarrow{OC}$=(-1,-3),
故答案为:(-1,-3).
点评 本题考查向量的坐标运算,向量的求模公式,综合性较强,解决本题关键是认识到角平分线与向量的关系,求出$\overrightarrow{OB}$方向上的单位向量,用待定系数法将向量$\overrightarrow{OC}$表示出来,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
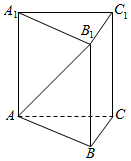 正三棱柱ABC-A1B1C1的底面边长为a,AA1=$\sqrt{2}$a,求:
正三棱柱ABC-A1B1C1的底面边长为a,AA1=$\sqrt{2}$a,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com