
已知点 ,直线
,直线 ,动点
,动点 到点
到点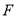 的距离等于它到直线
的距离等于它到直线 的距离.
的距离.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)是否存在过 的直线
的直线 ,使得直线
,使得直线 被曲线
被曲线 截得的弦
截得的弦 恰好被点
恰好被点 所平分?
所平分?
(1)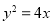 ;(2)
;(2)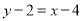 即
即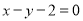
【解析】
试题分析:(1)求抛物线标准方程的常用方法是待定系数法,其关键是判断焦点位置,开口方向,在方程的类型已经确定的前提下,由于标准方程只有一个参数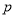 ,只需一个条件就可以确定抛物线的标准方程,或根据定义来求抛物线方程.(2)在解决与抛物线性质有关的问题时,要注意利用几何图形的形象、直观的特点来解题,特别是涉及焦点、顶点、准线的问题更是如此;(3)求双曲线的标准方程的基本方法是待定系数法,具体过程是先定形,再定量,即先确定双曲线标准方程的形式,求出
,只需一个条件就可以确定抛物线的标准方程,或根据定义来求抛物线方程.(2)在解决与抛物线性质有关的问题时,要注意利用几何图形的形象、直观的特点来解题,特别是涉及焦点、顶点、准线的问题更是如此;(3)求双曲线的标准方程的基本方法是待定系数法,具体过程是先定形,再定量,即先确定双曲线标准方程的形式,求出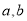 的值.
的值.
试题解析:(Ⅰ)因点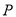 到点
到点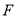 的距离等于它到直线
的距离等于它到直线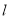 的距离,所以点
的距离,所以点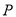 的轨迹
的轨迹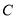 是以
是以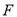 为焦点、直线
为焦点、直线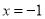 为准线的抛物线,
为准线的抛物线,
其方程为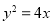 .
.
(Ⅱ)解法一:假设存在满足题设的直线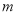 .设直线
.设直线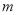 与轨迹
与轨迹 交于
交于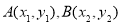 ,
,
依题意,得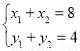 .
.
①当直线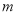 的斜率不存在时,不合题意.
的斜率不存在时,不合题意.
②当直线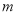 的斜率存在时,设直线
的斜率存在时,设直线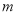 的方程为
的方程为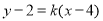 ,
,
联立方程组 ,
,
消去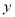 ,得
,得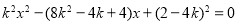 ,(*)
,(*)
∴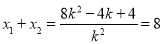 ,解得
,解得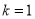 .
.
此时,方程(*)为 ,其判别式大于零,
,其判别式大于零,
∴存在满足题设的直线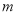
且直线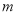 的方程为:
的方程为: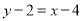 即
即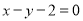 .
.
解法二:假设存在满足题设的直线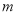 .设直线
.设直线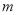 与轨迹
与轨迹 交于
交于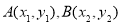 ,
,
依题意,得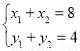 .
.
∵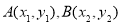 在轨迹
在轨迹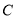 上,
上,
∴有 ,将
,将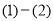 ,得
,得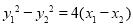 .
.
当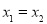 时,弦
时,弦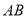 的中点不是
的中点不是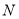 ,不合题意,
,不合题意,
∴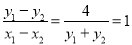 ,即直线
,即直线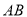 的斜率
的斜率 ,
,
注意到点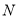 在曲线
在曲线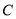 的张口内(或:经检验,直线
的张口内(或:经检验,直线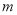 与轨迹
与轨迹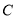 相交)
相交)
∴存在满足题设的直线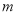
且直线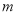 的方程为:
的方程为: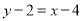 即
即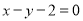 .
.
考点:(1)抛物线的标准方程;(2)直线与抛物线的综合问题.


科目:高中数学 来源:2015届福建省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知函数
 为自然对数的底数).
为自然对数的底数).
(1)求曲线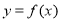 在
在 处的切线方程;
处的切线方程;
(2)若 是
是 的一个极值点,且点
的一个极值点,且点 ,
, 满足条件:
满足条件:
 .
.
(ⅰ)求 的值;
的值;
(ⅱ)求证:点 ,
, ,
, 是三个不同的点,且构成直角三角形.
是三个不同的点,且构成直角三角形.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期中考理科数学试卷(解析版) 题型:选择题
用0,1,2,3,4,5这六个数字组成没有重复数字的三位数,其中偶数共有
A.40个 B.42个 C.48个 D.52个
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末文科数学试卷(解析版) 题型:填空题
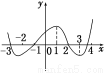
如图是y=f(x)的导函数的图象,现有四种说法:
(1)f(x)在(-3,1)上是增函数;
(2)x=-1是f(x)的极小值点;
(3)f(x)在(2,4)上是减函数,在(-1,2)上是增函数;
(4)x=2是f(x)的极小值点;
以上正确的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com