
 已知函数f(x)=x|x-2|.
已知函数f(x)=x|x-2|.分析 (1)作函数f(x)=x|x-2|的图象,从而解得.
(2)结合图象写出函数的单调性;
(3)结合图象可知f(x)=1的一个解为x=1,再解方程x(x-2)=1即可.
解答 解:(1)作函数f(x)=x|x-2|的图象如下,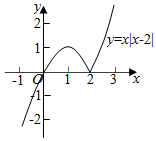
(2)结合图象可知,
f(x)在(-∞,1],[2,+∞)上单调递增,
在(1,2)上单调递减;
(3)结合图象可知,f(x)=1的一个解为x=1,
由x(x-2)=1解得,
x=1+$\sqrt{2}$,或x=1-$\sqrt{2}$(舍去);
故x的值为1或1+$\sqrt{2}$.
点评 本题考查了方程的根与函数的零点的关系应用及数形结合的思想应用,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
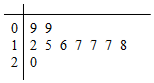 10名同学参加投篮比赛,每人投20球,投中的次数用茎叶图表示(如图),设其平均数为a,中位数为b,众数为c,则有( )
10名同学参加投篮比赛,每人投20球,投中的次数用茎叶图表示(如图),设其平均数为a,中位数为b,众数为c,则有( )| A. | a>b>c | B. | b>c>a | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com