【题目】已知椭圆
的中心在原点，焦点在坐标轴上，且经过
，
.
（Ⅰ）求椭圆的标准方程和离心率；
（Ⅱ）四边形
的四个顶点都在椭圆上，且对角线
，
过原点
，若
，求证：四边形的面积为定值，并求出此定值.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】先阅读下列不等式的证法，再解决后面的问题：
已知
，
，求证：
.
证明：构造函数
，
即
.
因为对一切
，恒有
，
所以
，从而得.
（1）若
，
，请写出上述结论的推广式；
（2）参考上述证法，对你推广的结论加以证明.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着人民生活水平的提高，对城市空气质量的关注度也逐步增大，图2是某城市1月至8月的空气质量检测情况，图中一、二、三、四级是空气质量等级， 一级空气质量最好，一级和二级都是质量合格天气，下面四种说法正确的是（ ）
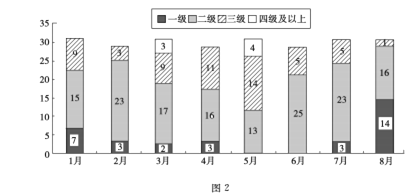
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比，空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】全国文明城市，简称文明城市，是指在全面建设小康社会中市民整体素质和城市文明程度较高的城市.全国文明城市称号是反映中国大陆城市整体文明水平的最高荣誉称号.为普及相关知识，争创全国文明城市，某市组织了文明城市知识竞赛，现随机抽取了甲、乙两个单位各5名职工的成绩（单位：分）如下表：
（1）根据上表中的数据，分别求出甲、乙两个单位5名职工的成绩的平均数和方差，并比较哪个单位的职工对文明城市知识掌握得更好；
（2）用简单随机抽样法从乙单位5名职工中抽取2人，求抽取的2名职工的成绩差的绝对值不小于4的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知,如图,在直二面角
中,四边形
是边长为
的正方形,
,且
.
（Ⅰ）求证:
平面
;
（Ⅱ）求二面角
的余弦值;
（Ⅲ）在线段
（不包含端点）上是否存在点
,使得
与平面
所成的角为
;若存在,写出
的值,若不存在,说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四棱锥
中，底面
是正方形，顶点
在底面的射影是底面的中心，且各顶点都在同一球面上，若该四棱锥的侧棱长为
，体积为4，且四棱锥的高为整数，则此球的半径等于（参考公式：
）（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系中，以原点为极点，以
轴的非负半轴为极轴且取相同的单位长度建立极坐标系，曲线
的极坐标方程为：
.
（1）若曲线
参数方程为：
（
为参数），求曲线的直角坐标方程和曲线的普通方程；
（2）若曲线参数方程为：
（
为参数），
，且曲线与曲线交点分别为
，
，求
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
