
分析 (1)由等差数列和三角形的内角和可得B=$\frac{π}{3}$,再由余弦定理可得cosA,可得A值,进而可得C值;
(2)由(1)的三个角,可设a=k,b=$\sqrt{3}$k,c=2k,k为正数,由等比数列解k的方程可得;
(3)由直角三角形的面积公式以及和圆的位置关系可得.
解答 解:(1)∵△ABC中,A,B,C成等差数列,
∴2B=A+C,再由A+B+C=π可得B=$\frac{π}{3}$,
又∵a2=b2+c2-$\sqrt{3}$bc,∴cosA=$\frac{\sqrt{3}}{2}$,
∴A=$\frac{π}{6}$,C=π-A-B=$\frac{π}{2}$;
(2)由(1)可得A=$\frac{π}{6}$,B=$\frac{π}{3}$,C=$\frac{π}{2}$,
∴由可设a=k,b=$\sqrt{3}$k,c=2k,k为正数,
又∵a,b,c+4成等比数列,
∴b2=a(c+4),∴3k2=k(2k+4),
解方程可得k=4,
∴a=4,b=4$\sqrt{3}$,c=8;
(3)∴△ABC的面积S=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$,
△ABC的外接圆半径R满足2R=8,解得R=4
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式,属中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:解答题
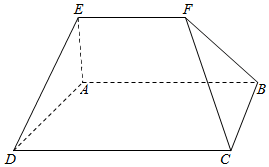 如图,用四种不同颜色的灯泡安装在图中的A,B,C,D,E,F六个点,要求每个点安装一个灯袍,且图中每条线段两个端点的灯泡颜色不同,则不同的安装方法共有多少种?
如图,用四种不同颜色的灯泡安装在图中的A,B,C,D,E,F六个点,要求每个点安装一个灯袍,且图中每条线段两个端点的灯泡颜色不同,则不同的安装方法共有多少种?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
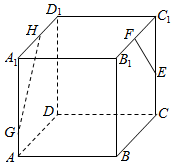 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别为边CC1、B1C1的中点,点G、H分别在AA1、D1A1上,且满足AA1=3AG,D1H=2HA1,则异面直线EF、GH所成角的余弦值为$\frac{\sqrt{10}}{10}$.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别为边CC1、B1C1的中点,点G、H分别在AA1、D1A1上,且满足AA1=3AG,D1H=2HA1,则异面直线EF、GH所成角的余弦值为$\frac{\sqrt{10}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
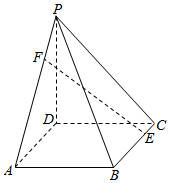 如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com