
分析 (1)当n≥2时,an=Sn-Sn-1=2n+3,从而再检验即可;
(2)化简cn=an•bn=(2n+3)•2n,从而利用错位相减法求和.
解答 解:(1)当n≥2时,an=Sn-Sn-1
=n2+4n-((n-1)2+4(n-1))
=2n+3,
当n=1时,a1=5也符合上式,
故an=2n+3;
(2)由(1)知,cn=an•bn=(2n+3)•2n,
Tn=5•2+7•4+9•8+…+(2n+3)•2n,
2Tn=5•4+7•8+9•16+…+(2n+3)•2n+1,
两式作差可得,
Tn=-10-2•4-2•8-2•16-…-2•2n+(2n+3)•2n+1
=(2n+3)•2n+1-2$\frac{4(1-{2}^{n-1})}{1-2}$-10
=(2n+1)•2n+1-2.
点评 本题考查了等差数列与等比数列的应用及分类讨论的思想与错位相减法的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
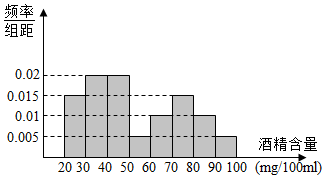 按规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含90)之间,属酒后驾车;在80mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.
按规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含90)之间,属酒后驾车;在80mg/100mL(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,如图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com