
分析 根据复数模的几何意义,将条件转化为距离问题即可得到结论.
解答 解:∵|z+2-2i|=|z-(-2+2i)|=1,
∴复数z的几何意义是复平面内的动点(x,y)到定点A(-2,2)的距离等于1,
对应的轨迹为以A为圆心,半径为1的圆;
|z-3-2i|=|z-(3+2i)|的几何意义是
z对应的点P到点B(3,2)的距离,
作出对应的图形,由图形知;
当点P位于C时,|z-3-2i|取得最小值,
|AB|=$\sqrt{{(-2-3)}^{2}{+(2-2)}^{2}}$=5,
∴|z-3-2i|的最小值为|AB|-r=5-1=4.
点评 本题主要考查复数的几何意义,利用两点间的距离公式是解题的关键,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{λ}{4}$ | B. | $\frac{λ}{2}$ | C. | λ | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
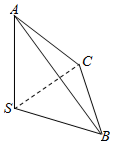 如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )
如图,三棱锥S-ABC中,棱SA,SB,SC两两垂直,且SA=SB=SC,则二面角A-BC-S大小的正切值为( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com