
分析 (1)根据圆的标准方程,设出点P的坐标,然后利用两点间距离公式,得到|AP|2+|BP|2的表达式,即可求得P点的坐标.
(2)①确定|QN|=|QM|,△QMN为等边三角形,即可求直线QC的方程;
②x2+y2-(a+3)x-4y+3a=0与圆C:x2+y2-6x-8y+21=0联立得:-a(x-3)+3x+4y-21=0,即可证明结论.
解答 解:(1)设P(x,y),由两点间的距离公式知:|AP|2+|BP|2=2(x2+y2)+2=2|OP|2+2.
又P为圆上的点,所以${|{OP}|_{min}}=|{OC}|-r=\sqrt{{3^2}+{4^2}}-2=3$,∴(|AP|2+|BP|2)min=20
此时直线$OC:y=\frac{4}{3}x$,由题意得:$\left\{\begin{array}{l}y=\frac{4}{3}x\\{({x-3})^2}+{({y-4})^2}=4\end{array}\right.$,∴P的坐标为$({\frac{9}{5},\frac{12}{5}})$;
(2)①设Q(x,0),因为圆C的半径r=2,而$|{MN}|=2\sqrt{3}$,
则$∠MCN=\frac{2π}{3}$,$∠MQN=\frac{π}{3}$
而|QN|=|QM|,△QMN为等边三角形.
∴|QC|2=|QN|2+|CN|2=16,∴|QC|=4,所求直线QC的方程:x=3
②$∠CNQ=∠CMQ=\frac{π}{2}$,则M,N在以QC为直径的圆上
设Q(a,0),则以QC为直径的圆的方程:${({x-\frac{a-3}{2}})^2}+{({y-2})^2}=\frac{{{{({a-2})}^2}+16}}{4}$
即x2+y2-(a+3)x-4y+3a=0与圆C:x2+y2-6x-8y+21=0联立得:-a(x-3)+3x+4y-21=0,
故无论a取何值时,直线MN恒过定点(3,3).
点评 本题考查了圆的方程的综合应用,和平面内两点间距离公式,考查圆与圆的位置关系,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
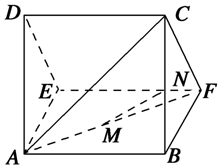 已知三棱柱ADE-BCF如图所示,其中M,N分别是AF,BC的中点,且平面ABCD⊥底面ABEF,AB=AD=AE=BF=BC=2.
已知三棱柱ADE-BCF如图所示,其中M,N分别是AF,BC的中点,且平面ABCD⊥底面ABEF,AB=AD=AE=BF=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
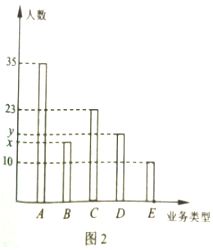 在某天的上午9:00~12:00时段,湛江一间商业银行随机收集了100位客户在营业厅窗口办理业务类型及用时量的信息,相关数据统计如表1与图2所示.
在某天的上午9:00~12:00时段,湛江一间商业银行随机收集了100位客户在营业厅窗口办理业务类型及用时量的信息,相关数据统计如表1与图2所示.| 一次办理业务类型 | A型业务 | B型业务 | C型业务 | D型业务 | E型业务 |
| 平均用时量(分钟/人) | 5 | 6.5 | 8 | 12 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{3}{4}$ | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com