
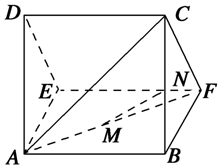
 已知三棱柱ADE-BCF如图所示,其中M,N分别是AF,BC的中点,且平面ABCD⊥底面ABEF,AB=AD=AE=BF=BC=2.
已知三棱柱ADE-BCF如图所示,其中M,N分别是AF,BC的中点,且平面ABCD⊥底面ABEF,AB=AD=AE=BF=BC=2.分析 (1)根据线面平行的判定定理进行证明即可.
(2)根据锥体的体积公式先求出锥体的底面积和高即可.
解答 (1)证明:由AB=BC=BF=2,DE=CF=2$\sqrt{2}$,∠CBF=$\frac{π}{2}$.
取BF的中点G,连接MG,NG,
由M,N分别为AF,BC的中点可得,
NG∥CF,MG∥EF,且NG∩MG=G,CF∩EF=F,
∴平面MNG∥平面CDEF,
又MN?平面MNG,
∴MN∥平面CDEF.-------------------------(6分)
(2)取DE的中点H.∵AD=AE,∴AH⊥DE,
在直三棱柱ADE-BCF中,平面ADE⊥平面CDEF,平面ADE∩平面CDEF=DE.
∴AH⊥平面CDEF.
∴多面体A-CDEF是以AH为高,以矩形CDEF为底面的棱锥,在△ADE中,AH=$\sqrt{2}$.
S矩形CDEF=DE•EF=4$\sqrt{2}$,
∴棱锥A-CDEF的体积为V=$\frac{1}{3}$•S矩形CDEF•AH=$\frac{1}{3}$×4$\sqrt{2}$×$\sqrt{2}$=$\frac{8}{3}$.----(12分)
点评 本题主要考查空间直线和平面平行的判定以及空间锥体的体积的计算,根据相应的判定定理和体积公式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知某路段最高限速60km/h,电子监控测得连续6辆汽车的速度用茎叶图表示如下(单位:km/h).若从中任取2辆,则恰好有1辆汽车超速的概率为( )
已知某路段最高限速60km/h,电子监控测得连续6辆汽车的速度用茎叶图表示如下(单位:km/h).若从中任取2辆,则恰好有1辆汽车超速的概率为( )| A. | $\frac{4}{15}$ | B. | $\frac{2}{5}$ | C. | $\frac{8}{15}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
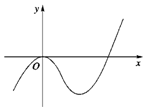 设函数f(x)=x3+ax2+bx+c的图象如图所示,且与y=0在原点相切,若函数的极小值为-4.
设函数f(x)=x3+ax2+bx+c的图象如图所示,且与y=0在原点相切,若函数的极小值为-4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com