练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知某路段最高限速60km/h，电子监控测得连续6辆汽车的速度用茎叶图表示如下（单位：km/h）．若从中任取2辆，则恰好有1辆汽车超速的概率为（　　）
    A．$\frac{4}{15}$B．$\frac{2}{5}$C．$\frac{8}{15}$D．$\frac{3}{5}$

    分析 求出基本事件的总数，满足题意的数目，即可求解概率．

    解答 解：不同车速有6辆，从中任取2辆，共有C62=15．
    则恰好有1辆汽车超速的数目：2×4=8．
    从中任取2辆，则恰好有1辆汽车超速的概率为：
    P=$\frac{8}{15}$．
    故选：C．

    点评 本题考查古典概型的概率的求法，基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．已知等差数列{an}满足：a5+a6+a7=15，Sn为数列{an}的前n项和，则S11=55．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．直线a∥平面β，直线a到平面β的距离为1，则到直线a的距离与平面β的距离都等于$\frac{4}{5}$的点的集合是（　　）
    A．一条直线B．一个平面C．两条平行直线D．两个平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

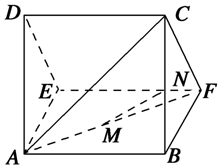    4．已知三棱柱ADE-BCF如图所示，其中M，N分别是AF，BC的中点，且平面ABCD⊥底面ABEF，AB=AD=AE=BF=BC=2．
    （1）求证：MN∥平面CDEF；
    （2）求多面体A-CDEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．抛物线y=x2-2x-3与坐标轴的交点在同一个圆上，则交点确定的圆的方程为（　　）
    A．x2+（y-1）2=2B．（x-1）2+（y-1）2=4C．（x-1）2+y2=4D．（x-1）2+（y+1）2=5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

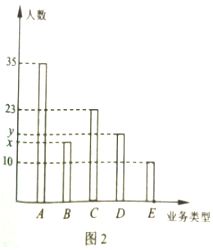    1．在某天的上午9：00～12：00时段，湛江一间商业银行随机收集了100位客户在营业厅窗口办理业务类型及用时量的信息，相关数据统计如表1与图2所示．
    一次办理业务类型A型业务B型业务C型业务D型业务E型业务
    平均用时量（分钟/人）56.581215
    已知这100位客户中办理型和型业务的共占50%（假定一人一次只办一种业务）．
    （Ⅰ）确定图2中x，y的值，并求随机一位客户一次办理业务的用时量X的分布列与数学期望；
    （Ⅱ）若某客户到达柜台时，前面恰有2位客户依次办理业务（第一位客户刚开始办理业务），且各客户之间办理的业务相互独立，求该客户办理业务前的等候时间不超过13分钟的概率．
    （注：将频率视为概率，参考数据：5×35+6.5×15+8×23+12×17=660.5，352+152+2×35×23+2×35×15=4110，352+152+35×23=2255）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．若数列{an}的通项公式是an=$\left\{\begin{array}{l}{{2}^{n+1}（1≤n≤2）}\\{\frac{1}{{3}^{n}}（n≥3）}\end{array}\right.$，前n项和为Sn，则$\underset{lim}{n→∞}$Sn的值为12$\frac{1}{18}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．圆x2+y2-2x-4y+1=0的圆心到直线ax+y-1=0的距离为1，则a=（　　）
    A．-$\frac{4}{3}$B．-$\frac{3}{4}$C．0D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知向量$\overrightarrow{a}$=（2，-1，2），$\overrightarrow{b}$=（-4，2，m），且$\overrightarrow{a}$∥$\overrightarrow{b}$，则m的值为-4．

    查看答案和解析>>

    同步练习册答案