【题目】已知曲线
的方程为
，集合
，若对于任意的
，都存在
，使得
成立，则称曲线为
曲线，下列方程所表示的曲线中，是曲线的有______（写出所有曲线的序号）
①
；②
；③
；④
；⑤
.
【答案】①③⑤
【解析】
对于任意
，存在
，使
成立，即
成立.①
表示的是椭圆，根据椭圆关于原点中心对称判断.②
表示双曲线，可取特殊点
判断.③
表示抛物线，根据其图象关于x轴对称判断.④根据其图形，可取特殊点
判断.⑤由
，可得
或点
，根据过原点一定有一条直线与之垂直来判断.
对于任意，存在，使成立，即.成立.
对于①，∵的图象关于原点中心对称，∴对于任意
，存在
，使.故为
曲线；
对于②，当
为双曲线的顶点时，双曲线上不存在点，使.故不是曲线；
对于③，其图象关于x轴对称，
的垂线一定与抛物线相交，故为曲线；
对于④，当为时，曲线上不存在点，使.故④不是曲线；
对于⑤，由可得或点，∴对于任意，存在，使.故为曲线.
故答案为:①③⑤.
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）当
时，直线
与
相切，求
的值；
（2）若函数在
内有且只有一个零点，求此时函数的单调区间；
（3）当
时，若函数在
上的最大值和最小值的和为1，求实数
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，曲线
过点
，其参数方程为
（
为参数， 
），以
为极点， 
轴非负半轴为极轴，建立极坐标系，曲线
的极坐标方程为
.
（1）求曲线
的普通方程和曲线
的直角坐标方程；
（2）求已知曲线
和曲线
交于
两点，且
，求实数
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】改革开放40年来，体育产业蓬勃发展反映了“健康中国”理念的普及．下图是我国2006年至2016年体育产业年增加值及年增速图．其中条形图表示体育产业年增加值（单位：亿元），折线图为体育产业年增长率（％）．
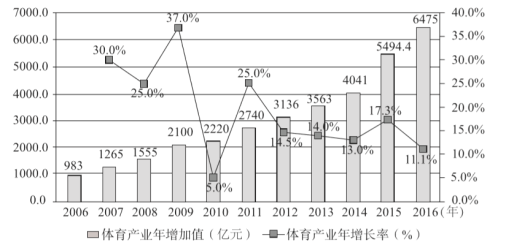
（Ⅰ）从2007年至2016年这十年中随机选出一年，求该年体育产业年增加值比前一年多
亿元以上的概率；
（Ⅱ）从2007年至2011年这五年中随机选出两年，求至少有一年体育产业年增长率超过25%的概率；
（Ⅲ）由图判断，从哪年开始连续三年的体育产业年增长率方差最大？从哪年开始连续三年的体育产业年增加值方差最大？（结论不要求证明）
查看答案和解析>>
科目：高中数学 来源： 题型：
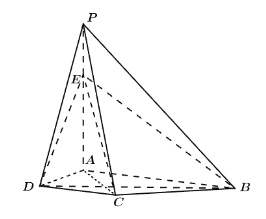
【题目】如图，在四棱锥
中，
平面
，
， 
，
，
，
，
为侧棱
上一点.
（Ⅰ）若
，求证：
平面
；
（Ⅱ）求证：平面
平面
；
（Ⅲ）在侧棱
上是否存在点
，使得
平面
？若存在，求出线段
的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分别随机抽取100个，并按[ 0，10]，（10，20]，（20，30]，（30，40]，（40，50]分组，得到频率分布直方图如下：
假设甲、乙两种酸奶独立销售且日销售量相互独立．
（1）写出频率分布直方图（甲）中的
的值；记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为
，
，试比较与的大小；（只需写出结论）
（2）估计在未来的某一天里，甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率；
（3）设
表示在未来3天内甲种酸奶的日销售量不高于20箱的天数，以日销售量落入各组的频率作为概率，求的数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线方程
，
为焦点，
为抛物线准线上一点，
为线段
与抛物线的交点，定义:
.
（1）当
时，求
；
（2）证明:存在常数
，使得
.
（3）
为抛物线准线上三点，且
，判断
与
的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
