【题目】已知
，设函数
.
（1）讨论
单调性；
（2）若当
时，
，求
的取值范围.
【答案】（1）见解析；（2）
【解析】
（1）求出函数
的导数，然后根据
的不同取值，进行分类讨论函数的单调性；
（2）当
时，
，且
时，
，于是
等价于
，显然若
，
时，不等式不成立；当若
，构造新函数
，求导，得
，函数
在
单调递增，所以
，可以证明出当
时，
，当
时，可以通过找到零点，证明出
不恒大于零.
解：（1）
.
当时，
，当
时，
，当
时，
.所以在
单调递增；在
单调递减.
当
时，由
得
或
，因为
，所以当或
时，，当
时，.所以在，
单调递增；在
单调递减.
（2）当时，，且时，，于是等价于.
若，当时，不成立.
若，设，.
函数在单调递增，所以.
当时，
，在单调递增，所以
.
当时，因为
，
，所以存在唯一
，使得当
时，
，在
单调递减，
，不成立.
综上，
的取值范围为
.
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案科目：高中数学 来源： 题型：
【题目】现代城市大多是棋盘式布局（如北京道路几乎都是东西和南北走向）.在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离（位移），而是实际路程（如图）.在直角坐标平面内，我们定义
，
两点间的“直角距离”为：
.
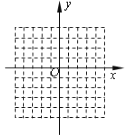
（1）在平面直角坐标系中，写出所有满足到原点的“直角距离”为2的“格点”的坐标.（格点指横、纵坐标均为整数的点）
（2）求到两定点
、
的“直角距离”和为定值
的动点轨迹方程，并在直角坐标系内作出该动点的轨迹.（在以下三个条件中任选一个做答）
①
，
，
；
②
，
，；
③，，
.
（3）写出同时满足以下两个条件的“格点”的坐标，并说明理由（格点指横、纵坐标均为整数的点）.
①到
，
两点“直角距离”相等；
②到
，
两点“直角距离”和最小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
是圆
：
上任意一点，
，线段
的垂直平分线与半径
交于点
，当点在圆上运动时，记点的轨迹为曲线
.
（1）求曲线的方程；
（2）记曲线与
轴交于
两点，
是直线
上任意一点，直线
，
与曲线的另一个交点分别为
，求证：直线
过定点
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线
的方程为
，集合
，若对于任意的
，都存在
，使得
成立，则称曲线为
曲线，下列方程所表示的曲线中，是曲线的有______（写出所有曲线的序号）
①
；②
；③
；④
；⑤
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某小学举办“父母养育我，我报父母恩”的活动，对六个年级（一年级到六年级的年级代码分别为1，2…，6）的学生给父母洗脚的百分比y%进行了调查统计，绘制得到下面的散点图．
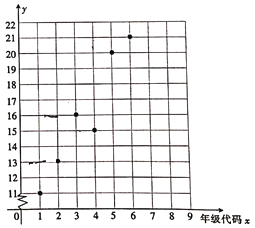
（1）由散点图看出，可用线性回归模型拟合y与x的关系，请用相关系数加以说明；
（2）建立y关于x的回归方程，并据此预计该校学生升入中学的第一年（年级代码为7）给父母洗脚的百分比．
附注：参考数据：
参考公式：相关系数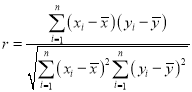
，若r＞0.95，则y与x的线性相关程度相当高，可用线性回归模型拟合y与x的关系．回归方程
中斜率与截距的最小二乘估计公式分别为
＝
，
．
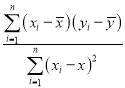查看答案和解析>>
科目：高中数学 来源： 题型：
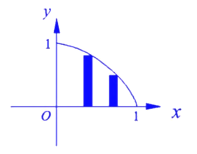
【题目】在平面直角坐标系中，函数
在第一象限内的图像如图所示，试做如下操作：把x轴上的区间
等分成n个小区间，在每一个小区间上作一个小矩形，使矩形的右端点落在函数的图像上.若用
表示第k个矩形的面积，
表示这n个叫矩形的面积总和.
（1）求
的表达式；
（2）利用数学归纳法证明
，并求出的表达式
（3）求
的值，并说明的几何意义.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
，其中
，点
是椭圆的右顶点，射线
：
与椭圆的交点为
.
（1）求点的坐标；
（2）设椭圆的长半轴、短半轴的长分别为
、
，当
的值在区间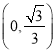
中变化时，求
的取值范围；
（3）在（2）的条件下，以为焦点，
为顶点且开口方向向左的抛物线过点，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，对于点
，若函数
满足：
，都有
，就称这个函数是点
的“限定函数”．以下函数：①
，②
，③
，④
，其中是原点
的“限定函数”的序号是______．已知点在函数
的图象上，若函数是点的“限定函数”，则
的取值范围是______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
