
【题目】在平面直角坐标系中,函数![]() 在第一象限内的图像如图所示,试做如下操作:把x轴上的区间
在第一象限内的图像如图所示,试做如下操作:把x轴上的区间![]() 等分成n个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数
等分成n个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数![]() 的图像上.若用
的图像上.若用![]() 表示第k个矩形的面积,
表示第k个矩形的面积,![]() 表示这n个叫矩形的面积总和.
表示这n个叫矩形的面积总和.
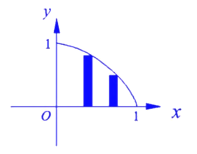
(1)求![]() 的表达式;
的表达式;
(2)利用数学归纳法证明![]() ,并求出
,并求出![]() 的表达式
的表达式
(3)求![]() 的值,并说明
的值,并说明![]() 的几何意义.
的几何意义.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】在信息时代的今天,随着手机的发展,“微信”越来越成为人们交流的一种方法,某机构对“使用微信交流”的态度进行调查,随机抽取了100人,他们年龄的频数分布及对“使用微信交流”赞成的人数如下表:(注:年龄单位:岁)
年龄 |
|
|
|
|
|
|
频数 | 10 | 30 | 30 | 20 | 5 | 5 |
赞成人数 | 9 | 25 | 24 | 9 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的![]() 列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() ,
,![]() 调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的“8”字形曲线是由两个关于![]() 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是![]() ,双曲线的左、右顶点
,双曲线的左、右顶点![]() 、
、![]() 是该圆与
是该圆与![]() 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与![]() 轴平行的直径的两端点.
轴平行的直径的两端点.
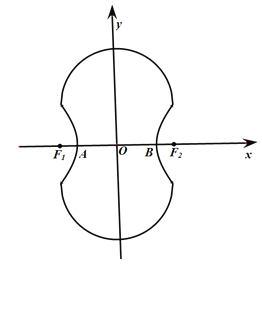
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为![]() 、
、![]() ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点![]() ,使得
,使得![]() 是直角.
是直角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,并按[ 0,10],(10,20],(20,30],(30,40],(40,50]分组,得到频率分布直方图如下:

假设甲、乙两种酸奶独立销售且日销售量相互独立.
(1)写出频率分布直方图(甲)中的![]() 的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为
的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(3)设![]() 表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求
表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,五边形![]() 中,四边形
中,四边形![]() 为长方形,
为长方形,![]() 为边长为
为边长为![]() 的正三角形,将
的正三角形,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 上的射影恰好在
上的射影恰好在![]() 上.
上.

(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的余弦值的绝对值.
所成二面角的余弦值的绝对值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,把长为6,宽为3的矩形折成正三棱柱![]() ,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱
,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱![]() 、
、![]() 的交点记为
的交点记为![]() .
.
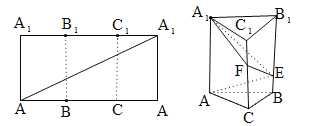
(1)在三棱柱![]() 中,若过
中,若过![]() 三点做一平面,求截得的几何体
三点做一平面,求截得的几何体![]() 的表面积;
的表面积;
(2)求三棱柱中异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是等差数列,
是等差数列,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求![]() 的通项公式;
的通项公式;
(2)求![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() 是等差数列,
是等差数列,![]() 与
与![]() 的公差不相等,且
的公差不相等,且![]() ,问:
,问:![]() 和
和![]() 中除第5项外,还有序号相同且数值相等的项吗?(直接写出结论即可)
中除第5项外,还有序号相同且数值相等的项吗?(直接写出结论即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com