[题目]微信支付诞生于微信红包.早期知识作为社交的一部分“发红包而诞生的.在发红包之余才发现.原来微信支付不仅可以用来发红包.还可以用来支付.现在微信支付被越来越多的人们所接受.现从某市市民中随机抽取300为对是否使用微信支付进行调查.得到下列的列联表:年轻人非年轻人总计经常使用微信支付165225不常使用微信支付合计90300 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】微信支付诞生于微信红包，早期知识作为社交的一部分“发红包”而诞生的，在发红包之余才发现，原来微信支付不仅可以用来发红包，还可以用来支付，现在微信支付被越来越多的人们所接受，现从某市市民中随机抽取300为对是否使用微信支付进行调查，得到下列的列联表：

	年轻人	非年轻人	总计
经常使用微信支付	165		225
不常使用微信支付
合计		90	300

根据表中数据，我们得到的统计学的结论是：由__________的把握认为“使用微信支付与年龄有关”。

其中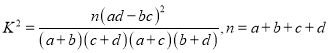

【答案】95%

【解析】由条件可得的列联表为：

	年轻人	非年轻人	总计
经常使用微信支付	165	60	225
不常使用微信支付	45	30	75
合计	210	90	300

∴，

∴有95%的把握认为“使用微信支付与年龄有关”。

答案：95%

练习册系列答案

练习册吉林教育出版集团有限责任公司系列答案

练习册湖北教育出版社系列答案

新课标同步练习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，四棱锥中，为正三角形，平面底面，底面为梯形，，，，，，点在棱上，且．　

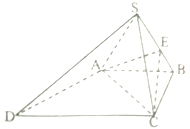
求证：（1）平面平面；

（2）求证：平面；

（3）求三棱锥的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知（为常数）．

（1）当时，求函数的单调性；

（2）当时，求证：；

（3）试讨论函数零点的个数．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：

	男	女	总计
爱好	40	20	60
不爱好	20	30	50
总计	60	50	110

由算得，．

P（K2≥k）	0.050	0.010	0.001
k	3.841	6.635	10.828

参照附表，得到的正确结论是（）
A.在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某服装厂生产一种服装，每件服装成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，规定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低元，根据市场调查，销售商一次订购不会超过600件.

（1）设一次订购件，服装的实际出厂单价为元，写出函数的表达式；

（2）当销售商一次订购多少件服装时，该厂获得的利润最大？其最大利润是多少？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设关于某产品的明星代言费x（百万元）和其销售额y（百万元），有如表的统计表格：

i	1	2	3	4	5	合计
xi（百万元）	1.26	1.44	1.59	1.71	1.82	7.82
wi（百万元）	2.00	2.99	4.02	5.00	6.03	20.04
yi（百万元）	3.20	4.80	6.50	7.50	8.00	30.00
=1.56， =4.01， =6， xiyi=48.66， wiyi=132.62，（xi﹣ ）2=0.20，（wi﹣ ）2=10.14

其中．
（1）在坐标系中，作出销售额y关于广告费x的回归方程的散点图，根据散点图指出：y=a+blnx，y=c+dx3哪一个适合作销售额y关于明星代言费x的回归类方程（不需要说明理由）；

（2）已知这种产品的纯收益z（百万元）与x，y有如下关系：x=0.2y﹣0.726x（x∈[1.00，2.00]），试写出z=f（x）的函数关系式，试估计当x取何值时，纯收益z取最大值？（以上计算过程中的数据统一保留到小数点第2位）