
【题目】已知椭圆 ![]() +y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足
+y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足 ![]() =
= ![]() .
.
(1)求证: ![]() +
+ ![]() =
= ![]() ;
;
(2)kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则,请说明理由.
【答案】
(1))证明:分别连接AB、BC、CD、AD,∵AC、BD相交于原点O,
根据椭圆的对称性可知,AC、BD互相平分,且原点O为它们的中点.
则四边形ABCD为平行四边形,故 ![]() ,即
,即 ![]() +
+ ![]() =
= ![]()
(2)解:∵ ![]() =
= ![]() ,∴4y1y2=x1x2,
,∴4y1y2=x1x2,
若直线AB的斜率不存在(或AB的斜率为0时),不满足4y1y2=x1x2;
直线AB的斜率存在且不为0时,设直线方程为y=kx+m,A(x1,y1),B(x2,y2).
联立 ![]() ,得(1+4k2)x2+8kmx+4(m2﹣1)=0.
,得(1+4k2)x2+8kmx+4(m2﹣1)=0.
△=(8km)2﹣4(1+4k2)(4m2﹣4)=16(4k2﹣m2+1)>0,①
![]() .
.
∵4y1y2=x1x2,又 ![]() ,
,
∴ ![]() ,
,
即 ![]() .
.
整理得:k= ![]() .
.
∵A、B、C、D的位置可以轮换,∴AB、BC的斜率一个是 ![]() ,另一个就是
,另一个就是 ![]() .
.
∴kAB+kBC= ![]() ,是定值.
,是定值.
不妨设 ![]() ,则
,则 ![]() .
.
设原点到直线AB的距离为d,则 ![]()
= ![]() ≤1.
≤1.
当m2=1时满足①取等号.
∴S四边形ABCD=4S△AOB≤4,即四边形ABCD面积的最大值为4
【解析】(1)由题意可得四边形ABCD为平行四边形,故 ![]() ,即
,即 ![]() +
+ ![]() =
= ![]() ;(2)由
;(2)由 ![]() =
= ![]() ,得4y1y2=x1x2 , 若直线AB的斜率不存在(或AB的斜率为0时),不满足4y1y2=x1x2;当直线AB的斜率存在且不为0时,设直线方程为y=kx+m,A(x1 , y1),B(x2 , y2).联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系求得A,B的横坐标的和与积,结合4y1y2=x1x2
,得4y1y2=x1x2 , 若直线AB的斜率不存在(或AB的斜率为0时),不满足4y1y2=x1x2;当直线AB的斜率存在且不为0时,设直线方程为y=kx+m,A(x1 , y1),B(x2 , y2).联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系求得A,B的横坐标的和与积,结合4y1y2=x1x2
求得k,把三角形AOB的面积化为关于m的函数,利用基本不等式求其最值,进一步得到四边形ABCD面积的最大值.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )已知双曲线
)已知双曲线![]() 的离心率是椭圆
的离心率是椭圆![]() 的离心率的倒数,其顶点为椭圆的焦点,求双曲线
的离心率的倒数,其顶点为椭圆的焦点,求双曲线![]() 的方程.
的方程.
(![]() )设直线
)设直线![]() 与双曲线交于
与双曲线交于![]() ,
, ![]() 两点,过
两点,过![]() 的直线
的直线![]() 与线段
与线段![]() 有公共点,求直线
有公共点,求直线![]() 的倾斜角的取值范围.
的倾斜角的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信支付诞生于微信红包,早期知识作为社交的一部分“发红包”而诞生的,在发红包之余才发现,原来微信支付不仅可以用来发红包,还可以用来支付,现在微信支付被越来越多的人们所接受,现从某市市民中随机抽取300为对是否使用微信支付进行调查,得到下列![]() 的列联表:
的列联表:
年轻人 | 非年轻人 | 总计 | |
经常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合计 | 90 | 300 |
根据表中数据,我们得到的统计学的结论是:由__________的把握认为“使用微信支付与年龄有关”。
|
|
|
|
|
|
|
|
|
|
|
|
其中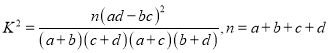
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上零点的个数;
上零点的个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在定义域内为增函数,求实数
在定义域内为增函数,求实数![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的极小值;
的极小值;
(3)设![]() ,
, ![]() .若函数
.若函数![]() 存在两个零点
存在两个零点![]() ,且满足
,且满足![]() ,问:函数
,问:函数![]() 在
在![]() 处的切线能否平行于
处的切线能否平行于![]() 轴?若能,求出该切线方程,若不能,请说明理由.
轴?若能,求出该切线方程,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为4的正方形ABCD的边上有动点P,动点P从B点开始沿折线BCDA运动到A终止,设P点移动的距离为x,![]() 的面积为S.
的面积为S.
(1)求函数S=f(x)的解析式、定义域,画出函数图像;
(2)求函数S=f(x)的值域. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com