
【题目】已知函数![]() .
.
(1)若函数![]() 在定义域内为增函数,求实数
在定义域内为增函数,求实数![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的极小值;
的极小值;
(3)设![]() ,
, ![]() .若函数
.若函数![]() 存在两个零点
存在两个零点![]() ,且满足
,且满足![]() ,问:函数
,问:函数![]() 在
在![]() 处的切线能否平行于
处的切线能否平行于![]() 轴?若能,求出该切线方程,若不能,请说明理由.
轴?若能,求出该切线方程,若不能,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)不能
(3)不能
【解析】试题分析:(1)先根据题意写出:g(x)再求导数,由题意知,g′(x)≥0,x∈(0,+∞)恒成立,即![]() ,n由此即可求得实数a的取值范围;
,n由此即可求得实数a的取值范围;
(Ⅱ)由(Ⅰ)知![]() ,利用换元法令t=ex,则t∈[1,2],则h(t)=t3-3at,接下来利用导数研究此函数的单调性,从而得出h(x)的极小值;
,利用换元法令t=ex,则t∈[1,2],则h(t)=t3-3at,接下来利用导数研究此函数的单调性,从而得出h(x)的极小值;
(Ⅲ)对于能否问题,可先假设能,即设F(x)在(x0,F(x0))的切线平行于x轴,其中F(x)=2lnx-x2-kx结合题意,列出方程组,证得函数![]() 在(0,1)上单调递增,最后出现矛盾,说明假设不成立,即切线不能否平行于x轴.
在(0,1)上单调递增,最后出现矛盾,说明假设不成立,即切线不能否平行于x轴.
试题解析:
解:(Ⅰ)![]()
由题意,知![]() 恒成立,即
恒成立,即![]()
又![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
故![]() ,所以
,所以![]() .
.
(Ⅱ)由(Ⅰ)知,![]() 令
令![]() ,则
,则![]() ,则
,则![]()
![]()
由![]() ,得
,得![]() 或
或![]() (舍去),
(舍去),![]() ,
,
①若![]() ,则
,则![]() 单调递减;
单调递减;![]() 在
在![]() 也单调递减;
也单调递减;
②若![]() ,则
,则![]() 单调递增.
单调递增. ![]() 在
在![]() 也单调递增;
也单调递增;
故![]() 的极小值为
的极小值为![]()
(Ⅲ)设![]() 在
在![]() 的切线平行于
的切线平行于![]() 轴,其中
轴,其中![]()
结合题意,有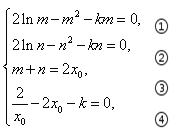
①-②得![]() ,所以
,所以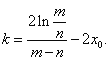 由④得
由④得![]()
所以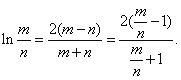 ⑤
⑤
设![]() ,⑤式变为
,⑤式变为![]()
设![]() ,
,
![]()
所以函数![]() 在
在![]() 上单调递增,因此,
上单调递增,因此,![]() ,即
,即![]()
也就是,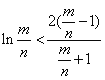 ,此式与⑤矛盾.
,此式与⑤矛盾.
所以![]() 在
在![]() 处的切线不能平行于
处的切线不能平行于![]() 轴.
轴.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足
+y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足 ![]() =
= ![]() .
.
(1)求证: ![]() +
+ ![]() =
= ![]() ;
;
(2)kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB是⊙O的直径,直线AF交⊙O于F(不与B重合),直线EC与⊙O相切于C,交AB于E,连接AC,且∠OAC=∠CAF,求证: 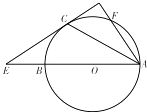
(1)AF⊥EC;
(2)若AE=5,AF=2,求AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin2x的图象,只需把函数y=sin(2x﹣ ![]() )的图象( )
)的图象( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由已知,利用正弦定理可得![]() a2=
a2=![]() b2+
b2+![]() c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
(2)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.
试题解析:
(1)因为![]() asin A=(
asin A=(![]() b-c)sin B+(
b-c)sin B+(![]() c-b)·sin C,
c-b)·sin C,
由正弦定理得![]() a2=(
a2=(![]() b-c)b+(
b-c)b+(![]() c-b)c,
c-b)c,
整理得![]() a2=
a2=![]()
![]() c2-2bc,
c2-2bc,
由余弦定理得cos A=![]() =
=![]() =
=![]() ,
,
因为A∈(0,π),所以A=![]() .
.
(2)由cos B=![]() ,得sin B=
,得sin B=![]() =
=![]() =
=![]() ,
,
所以cos C=cos[π-(A+B)]=-cos(A+B)=-![]() =-
=-![]() ,
,
由正弦定理得b=![]() =
=![]() =2,
=2,
所以CD=![]() AC=1,
AC=1,
在△BCD中,由余弦定理得BD2=(![]() )2+12-2×1×
)2+12-2×1×![]() ×
×![]() =13,
=13,
所以BD=![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 给出下列四个命题:
给出下列四个命题:
①c = 0时,![]() 是奇函数; ②
是奇函数; ②![]() 时,方程
时,方程![]() 只有一个实根;
只有一个实根;
③![]() 的图象关于点(0 , c)对称; ④方程
的图象关于点(0 , c)对称; ④方程![]() 至多3个实根.
至多3个实根.
其中正确的命题个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,角A,B,C的对边分别为a,b,c,R表示
中,角A,B,C的对边分别为a,b,c,R表示![]() 的外接圆半径.
的外接圆半径.
(Ⅰ)如图,在以O圆心、半径为2的![]() O中,BC和BA是
O中,BC和BA是![]() O的弦,其中
O的弦,其中![]() ,求弦AB的长;
,求弦AB的长;
(Ⅱ)在![]() 中,若
中,若![]() 是钝角,求证:
是钝角,求证:![]() ;
;
(Ⅲ)给定三个正实数a、b、R,其中![]() ,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的
,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的![]() 不存在、存在一个或存在两个(全等的三角形算作同一个)?在
不存在、存在一个或存在两个(全等的三角形算作同一个)?在![]() 存在的情况下,用a、b、R表示c.
存在的情况下,用a、b、R表示c.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com