
【题目】已知![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)解关于![]() 的不等式
的不等式![]() ,结果用集合或区间表示.
,结果用集合或区间表示.
【答案】(1)0
(2)![]()
(3)当a>1时,不等式的解集为(1-loga2,1+loga5);当0<a<1时,不等式的解集为R.
【解析】
试题分析:解 (1)∵f(x)是奇函数,∴f(-2)=-f(2),即f(2)+f(-2)=0.
(2)当x<0时,-x>0,∴f(-x)=a-x-1.
∵f(x)是奇函数,有f(-x)=-f(x),∴f(x)=-a-x+1(x<0).
∴所求的解析式为![]() .
.
(3)不等式等价于![]() 或
或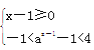 ,
,
即![]() 或
或![]() .
.
当a>1时,有![]() 或
或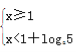 ,注意此时loga2>0,loga5>0,
,注意此时loga2>0,loga5>0,
可得此时不等式的解集为(1-loga2,1+loga5).
同理可得,当0<a<1时,不等式的解集为R.
综上所述,当a>1时,不等式的解集为(1-loga2,1+loga5);当0<a<1时,不等式的解集为R.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足
+y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足 ![]() =
= ![]() .
.
(1)求证: ![]() +
+ ![]() =
= ![]() ;
;
(2)kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 给出下列四个命题:
给出下列四个命题:
①c = 0时,![]() 是奇函数; ②
是奇函数; ②![]() 时,方程
时,方程![]() 只有一个实根;
只有一个实根;
③![]() 的图象关于点(0 , c)对称; ④方程
的图象关于点(0 , c)对称; ④方程![]() 至多3个实根.
至多3个实根.
其中正确的命题个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
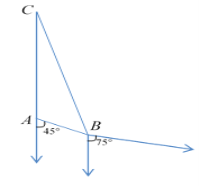
【题目】如图,在海岸A处,发现南偏东45°方向距A为(2![]() -2)海里的B处有一艘走私船,在A处正北方向,距A为
-2)海里的B处有一艘走私船,在A处正北方向,距A为![]() 海里的C处的缉私船立即奉命以10
海里的C处的缉私船立即奉命以10![]() 海里/时的速度追截走私船.
海里/时的速度追截走私船.
(1)刚发现走私船时,求两船的距离;
(2)若走私船正以10![]() 海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:
海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:![]() ≈1.4,
≈1.4,![]() ≈2.5).
≈2.5).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex(ax2﹣x﹣1)(a∈R).
(1)若函数f(x)在R上单调递减,求a的取值范围
(2)当a>0时,求f(|sinx|)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求四棱锥![]() 的体积;
的体积;
(2)求证: ![]() ;
;
(3)判断线段![]() 上是否存在一点
上是否存在一点![]() (与点
(与点![]() 不重合),使得
不重合),使得![]() 四点共面? (结论不要求证明)
四点共面? (结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,角A,B,C的对边分别为a,b,c,R表示
中,角A,B,C的对边分别为a,b,c,R表示![]() 的外接圆半径.
的外接圆半径.
(Ⅰ)如图,在以O圆心、半径为2的![]() O中,BC和BA是
O中,BC和BA是![]() O的弦,其中
O的弦,其中![]() ,求弦AB的长;
,求弦AB的长;
(Ⅱ)在![]() 中,若
中,若![]() 是钝角,求证:
是钝角,求证:![]() ;
;
(Ⅲ)给定三个正实数a、b、R,其中![]() ,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的
,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的![]() 不存在、存在一个或存在两个(全等的三角形算作同一个)?在
不存在、存在一个或存在两个(全等的三角形算作同一个)?在![]() 存在的情况下,用a、b、R表示c.
存在的情况下,用a、b、R表示c.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)是定义在(0,+∞)上的增函数,且对一切x,y>0,满足![]() .
.
(1)求f(1)的值;
(2)若f(6)=1,解不等式f(x+3)-f(![]() )<2.
)<2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com