
已知两条不同的直线m、n,两个不同的平面a、β,则下列命题中的真命题是( )
| A.若m⊥a,n⊥β,a⊥β,则m⊥n | B.若m⊥a,n∥β,a⊥β,则m⊥n |
| C.若m∥a,n∥β,a∥β,则m∥n | D.若m∥a,n⊥β,a⊥β,则m∥n |
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:解答题
(方案二)如图是一个长方体被削去一部分后的多面体的直观图,它的正视图和侧视图已经画出.(单位:cm).
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅱ)(普通高中做)求三棱锥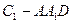 的体积.
的体积.
(示范性高中做)求多面体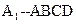 的体积.
的体积.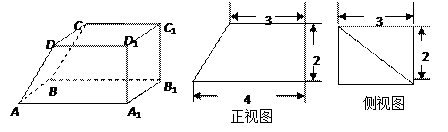
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)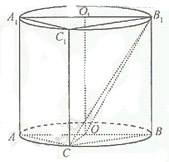
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,
三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径。
(Ⅰ)证明:平面A1ACC1⊥平面B1BCC1;
(Ⅱ)设AB=AA1。在圆柱OO1内随机选取一点,记该点取自于
三棱柱ABC-A1B1C1内的概率为P。
(i) 当点C在圆周上运动时,求P的最大值;
记平面A1ACC1与平面B1OC所成的角为 (0°<
(0°< 
 90°)。当P取最大值时,求cos
90°)。当P取最大值时,求cos 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
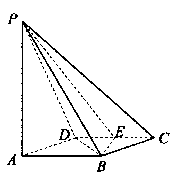
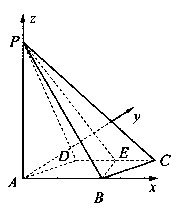
如图所示,四棱锥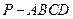 的底面
的底面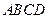 是边长为1的菱形,
是边长为1的菱形,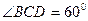 ,
,
E是CD的中点,PA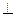 底面ABCD,
底面ABCD,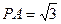 。
。
(I)证明:平面PBE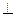 平面PAB;
平面PAB;
(II)求二面角A—BE—P和的大小。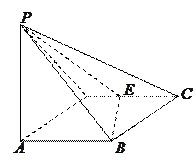
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图是一个正方体的展开图,如果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在的直线是异面直线的有( )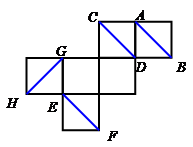
| A.1对 | B.2对 | C.3对 | D.4对 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知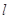 ,
,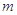 ,
,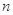 为三条不同的直线,
为三条不同的直线,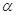 ,
,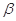 为两个不同的平面,下列命题中正确的是( )
为两个不同的平面,下列命题中正确的是( )
A.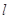 ⊥ ⊥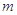 , ,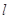 ⊥ ⊥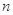 ,且 ,且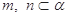 ,则 ,则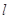 ⊥ ⊥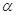 . . |
B.若平面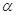 内有不共线的三点到平面 内有不共线的三点到平面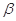 的距离相等,则 的距离相等,则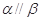 . . |
C.若 , ,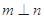 ,则 ,则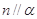 . . |
D.若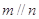 , ,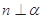 ,则 ,则 . . |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列四个命题中,正确命题的个数是( )个
① 若平面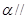 平面
平面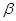 ,直线
,直线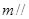 平面
平面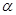 ,则
,则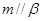 ;
;
② 若平面 平面
平面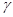 ,且平面
,且平面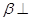 平面
平面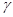 ,则
,则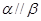 ;
;
③平面 平面
平面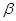 ,且
,且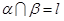 ,点
,点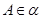 ,
, ,若直线
,若直线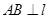 ,则
,则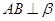 ;
;
④直线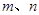 为异面直线,且
为异面直线,且 平面
平面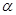 ,
,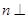 平面
平面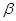 ,若
,若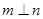 ,则
,则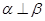 .
.
A. | B. | C.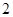 | D.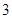 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.(本小题满分6分)
如图是一个几何体的三视图(单位:cm)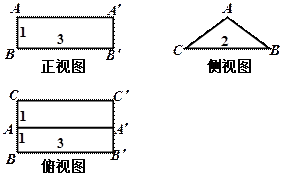
(Ⅰ)画出这个几何体的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积及体积;
(Ⅲ)设异面直线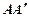 与
与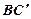 所
所 成的角为
成的角为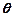 ,求
,求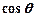 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com