【题目】设
是定义在
上的奇函数，当
时， 
.
（1）求
的解析式；
（2）解不等式
.
【答案】(1)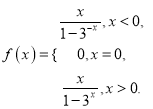 
；(2)(－∞，－2)∪(0,2)．
【解析】试题分析：（1）奇函数有f(0)＝0，再由x<0时，f(x)＝－f(－x)即可求解；
（2）由（1）分段求解不等式，最后取并集即可.
试题解析：
（1）因为f(x)是定义在
上的奇函数，所以当x=0时，f(x)＝0，
当x<0时，f(x)＝－f(－x)，－x>0，又因为当x>0时，f(x)＝
，.
所以当x<0时，f(x)＝－f(－x)＝－
＝
..
综上所述：此函数的解析式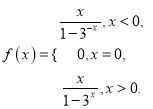
.
（2）f(x)<－
，当x=0时，f(x)<－不成立；
当x>0时，即<－，所以
<－
，所以
>，所以3x－1<8，解得x<2，
当x<0时，即<－，所以
>－，所以3－x>32，所以x<－2，
综上所述解集是(－∞，－2)∪(0,2)．
科目：高中数学 来源： 题型：
【题目】现有同一型号的电脑96台,为了了解这种电脑每开机一次所产生的辐射情况,从中抽取10台在同一条件下做开机实验,测量开机一次所产生的辐射,得到如下数据:
13.7 12.9 14.4 13.8 13.3
12.7 13.5 13.6 13.1 13.4
(1)写出采用简单随机抽样抽取上述样本的过程;
(2)根据样本,请估计总体平均数与总体标准差的情况.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】四边形OABC的四个顶点坐标分别为O(0,0)、A(6,2)、B(4,6)、C(2,6)，直线y＝kx(
<k<3)分四边形OABC为两部分，S表示靠近x轴一侧的那一部分的面积．
(1)求S＝f(k)的函数表达式；
(2)当k为何值时，直线y＝kx将四边形OABC分为面积相等的两部分？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，直线l的参数方程为 
（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12．
（Ⅰ）求曲线C的直角坐标方程；
（Ⅱ）已知直线l与曲线C交于A，B两点，试求|AB|．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且（a﹣c）（sinA+sinC）=（a﹣b）sinB．
（1）求角C的大小；
（2）若c= 
≤a，求2a﹣b的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}满足a1=2，an+1=an2+6an+6（n∈N×）
（1）设Cn=log5（an+3），求证{Cn}是等比数列；
（2）求数列{an}的通项公式；
（3）设bn= 
﹣ 
，数列{bn}的前n项和为Tn ， 求证：﹣ 
≤Tn＜﹣ 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C的圆心在直线3x+y﹣1=0上，且圆C在x轴、y轴上截得的弦长AB和MN分别为 
和 
．
（1）求圆C的方程；
（2）若圆心C位于第四象限，点P（x，y）是圆C内一动点，且x，y满足 
，求 
的范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
