【题目】已知圆C的圆心在直线3x+y﹣1=0上，且圆C在x轴、y轴上截得的弦长AB和MN分别为 
和 
．
（1）求圆C的方程；
（2）若圆心C位于第四象限，点P（x，y）是圆C内一动点，且x，y满足 
，求 
的范围．
【答案】
（1）解：设圆心为（a，b），半径为r，
则有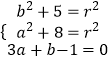 
得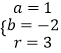 
或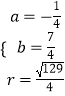 
，
圆C：（x﹣1）2+（y+2）2=9或 
（2）解：∵圆心C在第四象限，∴圆C的方程为（x﹣1）2+（y+2）2=9，
∴ 
， 
，
∴ 
，
∵x，y满足 
，
∴ 
（或 
），
又∵P在圆C内，满足（x﹣1）2+（y+2）2＜9且
∴4y2+8y﹣5＜0，解得 
，
∴ 
．
∴ 
的范围[﹣ 
，10）
【解析】（1）设出圆的圆心与半径，根据题意列出方程组，解方程组即可求得圆的方程；（2）根据圆心的象限位置确定圆的具体方程及点A，B的具体坐标，然后用x，y表示出
，再结合x，y的关系与点P在圆C内求得其取值范围.
【考点精析】通过灵活运用直线与圆的三种位置关系，掌握直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点即可以解答此题．
科目：高中数学 来源： 题型：
【题目】对于数列
，设
表示数列
前
项
， 
， 
， 
中的最大项．数列
满足： 
．
（
）若
，求
的前
项和．
（
）设数列
为等差数列，证明： 
或者
（
为常数），
， 
， 
， 
．
（
）设数列
为等差数列，公差为
，且
．
记
，
求证：数列
是等差数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x3﹣3ax． （Ⅰ）若函数f（x）在x=1处的切线斜率为2，求实数a；
（Ⅱ）若a=1，求函数f（x）在区间[0，3]的最值及所对应的x的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设等差数列{an}的前n项和为S，a2+a6=20，S5=40．
（1）求{an}的通项公式；
（2）设等比数列{bn}满足b2=a3 ， b3=a7．若b6=ak ， 求k的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合A={x|4x﹣1|＜9，x∈R}，B={x| 
≥0，x∈R}，则（RA）∩B=（ ）
A.（﹣∞，﹣3）∪[ 
，+∞）
B.（﹣3，﹣2]∪[0， ）??
C.（﹣∞，﹣3]∪[ ，+∞）
D.（﹣3，﹣2]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知四边形
是正方形， 
， 
， 
， 
都是等边三角形， 
、
、
、
分别是线段
、
、
、
的中点，分别以
、
、
、
为折痕将四个等边三角形折起，使得
、
、
、
四点重合于一点
，得到一个四棱锥．对于下面四个结论：
①
与
为异面直线； ②直线
与直线
所成的角为
③
平面
； ④平面
平面
；
其中正确结论的个数有（ ）
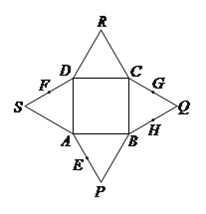
A. 
个 B. 
个 C. 
个 D. 
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
