
分析 ①、分2种情况讨论:当x≥0时和x<0时,分别将不等式变形化简,求出每种情况下不等式的解集,求其并集即可得答案.
②、根据题意,原不等式化为:a(x+a)(x-3)≤0,对a进行分情况讨论,综合即可得答案.
解答 解:①(1+x)(1-|x|)>0;
当x≥0时,
原不等式变形为(1+x)(1-x)>0,解可得-1<x<1,
则此时不等式的解集为{x|0≤x<1};
当x<0时,
原不等式变形为(1+x)(1+x)>0,恒成立
此时不等式的解集为{x|x<0};
综合可得:原不等式的解集为{x|x<1且x≠-1}.
②根据题意,原不等式化为:a(x+a)(x-3)≤0,
对a进行分情况讨论:
1、当a=0时,其解集为:R;
2、当a>0时,其解集为:{x|-a≤x≤3};
3、当-3<a<0时,其解集为:{x|x≤-a或x≥3};
4、当a<-3时,其解集为:{x|x≤3或x≥-a};
5、当a=-3时,其解集为:R.
点评 本题考查其他不等式的解法,注意②中需要对a进行分类讨论,做到不重不漏.


科目:高中数学 来源: 题型:选择题
| A. | R2的取值越小,模型拟合效果越好 | |
| B. | R2的取值可以任意大,且R2取值越大,拟合效果越好 | |
| C. | R2的取值越接近于1,模型拟合效果越好 | |
| D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
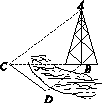 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=135°,CD=30m,并在点C处测得塔顶A的仰角为30°,则塔高AB
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=135°,CD=30m,并在点C处测得塔顶A的仰角为30°,则塔高AB| A. | 10$\sqrt{2}$ m | B. | 10$\sqrt{3}$ m | C. | 15$\sqrt{6}$ m | D. | 10$\sqrt{6}$ m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com