
分析 (1)由圆的方程求出圆心和半径,易得点A在圆外,当切线的斜率不存在时,切线方程为x=3.当切线的斜率存在时,设切线的斜率为k,写出切线方程,利用圆心到直线的距离等于半径,解出k,可得切线方程;
(2)当直线l⊥CN时,弦长最短,可求直线l的方程;
(3)求出轨迹C1,利用直线$y=k(x-\frac{5}{2})$与曲线C1只有一个交点,求k的值.
解答 解:(1)圆C:x2+y2-4x+3=0,即 (x-2)2+y2=1,表示以(2,0)为圆心,半径等于1的圆.
当切线的斜率不存在时,切线方程为x=3符合题意.
当切线的斜率存在时,设切线斜率为k,则切线方程为 y-2=k(x-3),即kx-y-3k+2=0,
所以,圆心到切线的距离等于半径,即$\frac{|-k+2|}{\sqrt{{k}^{2}+1}}$=1,解得k=$\frac{3}{4}$,此时,切线为3x-4y-1=0.
综上可得,圆的切线方程为x=3或3x-4y-1=0…(3分)
(2)直线l:2mx+2y-1-3m=0恒过定点$N({\frac{3}{2},\frac{1}{2}})$
当直线l⊥CN时,弦长最短,此时直线的方程为x-y-1=0…(7分)
(3)设点P(x,y),∵点P为线段AB的中点,曲线C是圆心为C(2,0),半径r=1的圆,∴CP⊥OP,$\overrightarrow{CP}•\overrightarrow{OP}=0$∴化简得(x-1)2+y2=1…(9分)
由于点P在圆内,由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-4x+3=0}\\{{x}^{2}+{y}^{2}-2x=0}\end{array}\right.$得x=$\frac{3}{2}$
所以C1:${({x-1})^2}+{y^2}=1({\frac{3}{2}<x≤2})$(注:范围也可写成$x>\frac{3}{2}$)…(10分)
圆心到直线的距离d=$\frac{|-\frac{3}{2}k|}{\sqrt{{k}^{2}+1}}$=1,∴$k=±\frac{{2\sqrt{5}}}{5}$,
过($\frac{3}{2}$,$\frac{\sqrt{5}}{2}$)时,k=$\frac{\sqrt{3}}{2}$
因为直线$y=k(x-\frac{5}{2})$与曲线C1只有一个交点,所以$-\frac{{\sqrt{3}}}{2}≤k≤\frac{{\sqrt{3}}}{2}$或$k=±\frac{{2\sqrt{5}}}{5}$…(12分)
点评 本题考查求圆的切线方程的方法,考查轨迹方程,考查点到直线距离公式的运用,属于中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 2 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
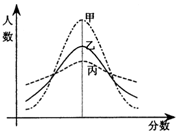 某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )
某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )| A. | 甲、乙、丙的总体的平均数不相同 | B. | 乙科总体的标准差及平均数都居中 | ||
| C. | 丙科总体的平均数最小 | D. | 甲科总体的标准差最小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com