
分析 根据点的坐标可求出向量$\overrightarrow{AC},\overrightarrow{BD}$的坐标,而根据投影的计算公式及向量夹角的余弦公式即可得出投影为:$\frac{\overrightarrow{AC}•\overrightarrow{BD}}{|\overrightarrow{BD}|}$,从而根据坐标即可求出该投影的值.
解答 解:$\overrightarrow{AC}=(-1,1),\overrightarrow{BD}=(3,2)$;
∴$\overrightarrow{AC}$在$\overrightarrow{BD}$方向上的投影为:
$|\overrightarrow{AC}|cos<\overrightarrow{AC},\overrightarrow{BD}>$=$|\overrightarrow{AC}|•\frac{\overrightarrow{AC}•\overrightarrow{BD}}{|\overrightarrow{AC}||\overrightarrow{BD}|}$
=$\frac{\overrightarrow{AC}•\overrightarrow{BD}}{|\overrightarrow{BD}|}$
=$\frac{-1}{\sqrt{13}}$
=$-\frac{\sqrt{13}}{13}$.
故答案为:$-\frac{\sqrt{13}}{13}$.
点评 考查根据点的坐标求向量坐标的方法,一个向量在另一个向量方向上的投影的定义及计算公式,以及向量数量积的坐标运算,根据向量坐标可求向量长度.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
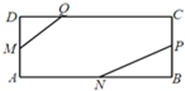 如图在长方形ABCD中,已知AB=4,BC=2,M,N,P为长方形边上的中点,Q是边CD上的点,且CQ=3DQ,求 $\overrightarrow{MQ}$•$\overrightarrow{NP}$的值.
如图在长方形ABCD中,已知AB=4,BC=2,M,N,P为长方形边上的中点,Q是边CD上的点,且CQ=3DQ,求 $\overrightarrow{MQ}$•$\overrightarrow{NP}$的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k) | … | 0.25 | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | … | 1.323 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com