（本小题满分12分）光线l过点P(1，－1)，经y轴反射后与圆C:(x－4)2+(y－
4)2=1
相切，求光线l所在的直线方程.
解：设l与y轴的交点(即反射点)为Q,点P关于y轴的对称点为P′(－1，－1).由
光学知识可知直线P′Q为反射线所在的直线，且为圆C的切线. ………………………2分
设P′Q的方程为y+1
=k(x+1)，即kx－y+k－1="0," …………………………………4分
由于圆心C(4，4)到P′Q的距离等于半径长，
∴
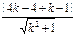=1.解得k=
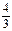或k=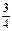
.…………………………………8分
由l与P′Q关于y轴对称可得l的斜率为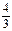－或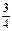－，…………………………10分
∴光线l所在的直线方程为y+1=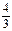－ (x－1)或y+1=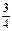－ (x－1),
即4x+3y－1=0或3x+4y+1="0." ………………………………12分
解析
科目：高中数学 来源： 题型：解答题
（13分） 已知圆
，
内接于此圆，
点的坐标
，
为坐标原点．
（Ⅰ）若的重心是
,求直线
的方程；
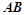（Ⅱ）若直线
与直线
的倾斜角互补，求证：直线的斜率为定值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（12分）已知点P到两个定点M(－1,0)，
N(1,0)的距离的比为。
（1）求证点P在一定圆上，并求此圆圆心和半径；
（2）若点N到直线PM的距离为1，求直线PN的方程。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）已知：以点
为圆心的圆与x轴交于
点O，A，与y轴交于点O，B，其中O为原点。
(Ⅰ) 求证：⊿OAB的面积为定值；
(Ⅱ) 设直线y=-2x+4与圆C交于点M，N，若OM=ON,求圆C的方程。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题12分）已知圆C经过点A（1，—1），B（—2，0），C（
，1）直线
:
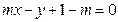
（1）求圆C的方程；
（2）求证：
，直线与圆C总有两个不同的交
点；
（3）若直线与圆C交于M、N两点，当
时，求m的值。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分10分）选修4－1：几何证明选讲
如图，直线AB过圆心O，交圆O于A、B，直线AF交圆O于F（不与B重合），直线
与圆O相切于C，交AB于E，且与AF垂直，垂足为G，连接AC．
求证：（Ⅰ）
；
（Ⅱ）
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
和
.
上，求圆的方程。
的渐近线与圆
相切，则双曲线离心率为（ ）.
.求 圆C的方程.