
分析 (1)方程f (x)=kx2有四个不同的实数解,代入函数表达式,进行探究,由于方程带有绝对值,故需要分类去绝对值,在每一类中找出满足方程有两解的参数的值,合并可得;
(2)关于x的方程$\frac{|x|}{x+4}$=kx2①由方程的形式可以看出,x=0恒为原方程①的一个解,即有|x|(x+4)=$\frac{1}{k}$(x≠0),画出y=|x|(x+4)的图象,对k讨论,再由二次方程的解法,即可得到所求解.
解答 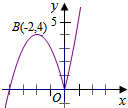 解:(1)原方程$\frac{|x|}{x+4}$=kx2①,
解:(1)原方程$\frac{|x|}{x+4}$=kx2①,
由方程的形式可以看出,x=0恒为原方程①的一个解.
当x<0且x≠-4时方程①有解,则$\frac{-x}{x+4}$=kx2即kx2+4kx+1=0,
当k=0时,方程kx2+4kx+1=0无解;
当k≠0时,△=16k2-4k≥0即k<0或k≥$\frac{1}{4}$时,方程kx2+4kx+1=0有解.
设方程kx2+4kx+1=0的两个根分别是x1,x2则x1+x2=-4,x1x2=$\frac{1}{k}$.
当k>$\frac{1}{4}$时,方程kx2+4kx+1=0有两个不等的负根;
当k=$\frac{1}{4}$时,方程kx2+4kx+1=0有两个相等的负根;
当k<0时,方程kx2+2kx+1=0有一个负根;
③当x>0时,方程①有解,则$\frac{x}{x+4}$=kx2,kx2+4kx-1=0,
当k=0时,方程kx2+4kx-1=0无解;
当k≠0时,△=16k2+4k≥0即k>0或k≤-$\frac{1}{4}$时,方程kx2+4kx-1=0有解.
设方程kx2+4kx-1=0的两个根分别是x3,x4
∴x3+x4=-4,x3x4=-$\frac{1}{k}$,
∴当k>0时,方程kx2+4kx-1=0有一个正根,
当k≤-$\frac{1}{4}$时,方程kx2+4kx-1=0没有正根.
综上可得,当k∈($\frac{1}{4}$,+∞)时,方程f (x)=kx2有四个不同的实数解.
(2)关于x的方程$\frac{|x|}{x+4}$=kx2①
由方程的形式可以看出,x=0恒为原方程①的一个解
即有|x|(x+4)=$\frac{1}{k}$(x≠0),
画出y=|x|(x+4)的图象,
当x=-2时,y=4,即B(-2,4),
1)当k=0时,方程的解为x=0;
2)当k<0时,当x<0时,-x(x+4)=$\frac{1}{k}$,
解得x=-2-$\sqrt{4-\frac{1}{k}}$,
方程的解为x=0或x=-2-$\sqrt{4-\frac{1}{k}}$;
3)当k>$\frac{1}{4}$时,方程有4个解.
当x>0时,由x(x+4)=$\frac{1}{k}$,可得x=-2+$\sqrt{4+\frac{1}{k}}$;
当x<0时,由-x(x+4)=$\frac{1}{k}$,可得x=-2±$\sqrt{4-\frac{1}{k}}$,
即有方程的解为x=0或x=-2+$\sqrt{4+\frac{1}{k}}$或x=-2±$\sqrt{4-\frac{1}{k}}$;
4)当0<k<$\frac{1}{4}$时,方程有两解.
x>0时,x(x+4)=$\frac{1}{k}$,解得x=-2+$\sqrt{4+\frac{1}{k}}$.
即有方程的解为x=0或x=-2+$\sqrt{4+\frac{1}{k}}$.
点评 本题考查方程的根的判断和求解,考查函数和方程的关系,注意运用分类讨论和数形结合的思想方法,考查运算求解能力,属于中档题和易错题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a2+b2≠0,则a≠0,b≠0 | B. | 若a2+b2≠0,则a≠0或b≠0 | ||
| C. | 若a2+b2=0,则a≠0,b≠0 | D. | 若a2+b2=0,则a≠0或b≠0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,1) | B. | (1,2) | C. | (1,2] | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com