练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列两个变量之间的关系哪个不是函数关系（　　）
    A.角度和它的正切值
    B.人的右手一柞长和身高
    C.正方体的棱长和表面积
    D.真空中自由落体运动物体的下落距离和下落时间

    【答案】B
    【解析】解答：由正切函数y=tanx知，A是函数关系；人的右手一柞长和身高不是确定的关系，故不是函数关系；设正方体的棱长为a，则它的表面积S=6a2 ， C是函数关系；
    由物理知识知，自由落体运动物体的下落距离h和下落时间t满足h= gt2（t＞0），D是函数关系．
    故选B．
    分析：由函数的定义知，两个变量具有确定的关系，利用这一点可知B不是函数关系，再由正切函数、正方体的表面积公式和物理知识知A、C、D是函数关系．
    【考点精析】解答此题的关键在于理解函数的概念及其构成要素的相关知识，掌握函数三要素是定义域，对应法则和值域，而定义域和对应法则是起决定作用的要素，因为这二者确定后，值域也就相应得到确定，因此只有定义域和对应法则二者完全相同的函数才是同一函数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足al=﹣2，an+1=2an+4．

    （I）证明数列{an+4}是等比数列；

    （Ⅱ）求数列{|an|}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）的定义域为（﹣2，2），函数g（x）=f（x﹣1）+f（3﹣2x）．
    （1）求函数g（x）的定义域；
    （2）若f（x）是奇函数且在定义域内单调递减，求不等式g（x）≤0的解集

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）已知数列{an}是等差数列，且a1，a2（a1＜a2）分别为方程x2﹣6x+5=0的二根．

    （1）求数列{an}的前n项和Sn；

    （2）在（1）中，设bn=，求证：当c=﹣时，数列{bn}是等差数列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f（x）=1﹣,求解：（1）f（x）的值域；（2）证明f（x）为R上的增函数． ．
    （1）求f（x）的值域；
    （2）证明f（x）为R上的增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=lnx+ax2﹣ax+5，a∈R．
    （1）若函数f（x）在x=1处有极值，求实数a的值；
    （2）若函数f（x）在区间（0，+∞）内单调递增，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数．他们研究过如图所示的三角形数：
    将三角形数1，3，6，10，…记为数列{an}，将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}，可以推测：
    （1）b5=；
    （2）b2n﹣1= ．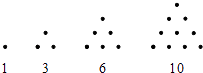

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，.

    （1）令，求的单调区间；

    （2）已知在处取得极大值，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知g（x）=sin2x，将g（x）的图象向左平移 个单位长度，再将图象上各点的横坐标缩短到原来的 ，得到函数f（x）的图象，则（ ）
    A.
    B. ??
    C.
    D.

    查看答案和解析>>

    同步练习册答案