
已知函数f(x)=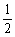 ax2-(2a+1)x+2lnx(a∈R).
ax2-(2a+1)x+2lnx(a∈R).
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)当a≤0时,求f(x)的单调区间。
解:函数f(x)的定义域为(0,+∞)
∵f ' (x)=ax-(2a+1)+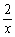
(1)由已知函数f ' (1)=f ' (3) a-(2a+1)+2=3a-(2a+1)+
a-(2a+1)+2=3a-(2a+1)+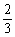
 a=
a=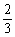
(2)f ' (x)=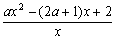 =
=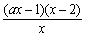 (x∈(0,+∞))
(x∈(0,+∞))
①当a=0时,f ' (x)=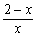 ,由f ' (x)>0得0<x<2,由f ' (x)<0得x>2
,由f ' (x)>0得0<x<2,由f ' (x)<0得x>2
∴f(x)在(0,2)上单调递增,在(2,+∞)上单调递减
②当a<0时,由f ' (x)=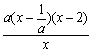 =0的x1=
=0的x1=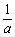 (舍去),x2=2,由f ' (x)>0的0<x<2,由f ' (x)<0的x>2
(舍去),x2=2,由f ' (x)>0的0<x<2,由f ' (x)<0的x>2
∴f(x)在(0,2)上单调递增,在(2,+∞)上单调递减
综上:当a≤0时,f(x)在(0,2)上单调递增,在(2,+∞)上单调递增


科目:高中数学 来源: 题型:
设A, B两点的坐标分别为(-1, 0), (1, 0),条件甲: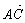 ·
·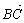 >0;条件乙:点C的坐
>0;条件乙:点C的坐
标是方程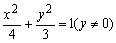 的解,则甲是乙的
的解,则甲是乙的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l, m,平面α,β, 且l⊥α, m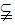 β,给出下列四个命题:
β,给出下列四个命题:
命题:
①若α∥β, 则l⊥m; ②若l⊥m, 则α∥β;
③若α⊥β,则l∥m; ④若l∥m, 则α⊥β
其中正确命题的序号是 。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax3+ x2在x=-1处取得极大值,记g(x)=
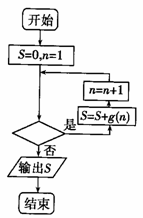
x2在x=-1处取得极大值,记g(x)=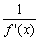 。程序框图如图所示,若输出的结果
。程序框图如图所示,若输出的结果
S=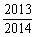 ,则判断框中可以填入的关于n的判断条件是
,则判断框中可以填入的关于n的判断条件是
A.n≤2013 B.n≤2014 C.n>2013 D.n>2014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com