
分析 运用直角三角形斜边的中线等于斜边的一半,可得AD=BD=5,即AB=10,再由勾股定理可得AC,再由$\overrightarrow{BD}$•$\overrightarrow{AC}$=-$\overrightarrow{AD}$•$\overrightarrow{AC}$,运用向量数量积的定义,计算即可得到所求值.
解答 解:在Rt△ABC中,D是斜边AB的中点,若BC=6,CD=5,
可得AD=BD=5,即AB=10,
由勾股定理可得AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,
则$\overrightarrow{BD}$•$\overrightarrow{AC}$=-$\overrightarrow{AD}$•$\overrightarrow{AC}$
=-|$\overrightarrow{AD}$|•|$\overrightarrow{AC}$|•cosA=-5×8×$\frac{8}{10}$=-32.
故答案为:-32.
点评 本题考查向量的数量积的定义,同时考查平面几何的性质:勾股定理和直角三角形斜边的中线等于斜边的一半,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>1 | B. | $m>\frac{1}{2}$ | C. | m>2 | D. | m≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20% | B. | 25% | C. | 40% | D. | 80% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
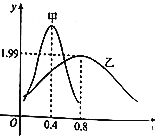 甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )| A. | 乙类水果的质量服从的正态分布的参数σ2=1.99 | |
| B. | 甲类水果的质量比乙类水果的质量更集中 | |
| C. | 甲类水果的平均质量μ1=0.4kg | |
| D. | 甲类水果的平均质量比乙类水果的平均质量小 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | 0 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com