
分析 (1)令f′(x)≤0在[3,5]上恒成立,分离参数得a≥2x2,利用二次函数的单调性求出最值即可得出a的范围;
(2)令g′(x)=0,根据根与系数的关系可得x1+x2=b-1,x1x2=1,化简得g(x1)-g(x2)=2ln$\frac{{x}_{1}}{{x}_{2}}$+($\frac{{x}_{2}}{{x}_{1}}$-$\frac{{x}_{1}}{{x}_{2}}$),令$\frac{{x}_{1}}{{x}_{2}}$=t,根据b的范围得出t的范围,利用函数单调性可求得h(t)=2lnt+($\frac{1}{t}$-t)的范围,得出结论.
解答 解:(1)∵f(x)=x2-alnx在[3,5]上是单调减函数,
∴f′(x)=2x-$\frac{a}{x}$≤0在[3,5]上恒成立,
∴a≥2x2恒成立,x∈[3,5].
∵y=2x2在[3,5]上单调递增,
∴y=2x2在[3,5]上的最大值为2×52=50,
∴a≥50.
(2)g(x)=x2-alnx+(2+a)lnx-2(b-1)x=x2+2lnx-2(b-1)x,
∴g′(x)=2x+$\frac{2}{x}$-2(b-1)=$\frac{2[{x}^{2}-(b-1)x+1]}{x}$,
令g′(x)=0得x2-(b-1)x+1=0,
∴x1+x2=b-1,x1x2=1,
∴g(x1)-g(x2)=[x12+2lnx1-2(b-1)x1]-[x22+2lnx2-2(b-1)x2]
=2ln$\frac{{x}_{1}}{{x}_{2}}$+(x12-x22)+2(b-1)(x2-x1)
=2ln$\frac{{x}_{1}}{{x}_{2}}$+(x12-x22)+2(x1+x2)(x2-x1)
=2ln$\frac{{x}_{1}}{{x}_{2}}$+x22-x12
=2ln$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{{x}_{2}}^{2}-{{x}_{1}}^{2}}{{x}_{1}{x}_{2}}$
=2ln$\frac{{x}_{1}}{{x}_{2}}$+($\frac{{x}_{2}}{{x}_{1}}$-$\frac{{x}_{1}}{{x}_{2}}$),
设$\frac{{x}_{1}}{{x}_{2}}$=t,则0<t<1,
∴g(x1)-g(x2)=2lnt+($\frac{1}{t}$-t),
令h(t)=2lnt+($\frac{1}{t}$-t),则h′(t)=$\frac{2}{t}$-$\frac{1}{{t}^{2}}$-1=-$\frac{(t-1)^{2}}{{t}^{2}}$<0,
∴h(t)在(0,1)上单调递减,
∵b≥$\frac{7}{2}$,∴(b-1)2≥$\frac{25}{4}$,即(x1+x2)2=$\frac{({x}_{1}+{x}_{2})^{2}}{{x}_{1}{x}_{2}}$=t+$\frac{1}{t}$+2≥$\frac{25}{4}$,
∴4t2-17t+4≥0,解得t≤$\frac{1}{4}$或t≥4.
又0<t<1,
∴0$<t≤\frac{1}{4}$.
∴hmin(t)=h($\frac{1}{4}$)=2ln$\frac{1}{4}$+(4-$\frac{1}{4}$)=$\frac{15}{4}$-4ln2.
∴g(x1)-g(x2)的最小值为$\frac{15}{4}$-4ln2.
点评 本题考查了导数与函数单调性的关系,函数最值的计算,利用根与系数的关系化简g(x1)-g(x2)是解题的关键点,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
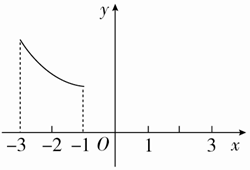 定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.
定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 乙 | ||||||||||||
| 8 | 9 | 9 | 8 | 9 | 9 | 3 | 8 | 9 | 9 | ||||
| 2 | 0 | 1 | 0 | 4 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com