
分析 (1)x2+2x+1-4m2=(x+1-2m)(x+1+2m)=0的两根为-1+2m,-1-2m,分-1+2m>-1-2m,1+2m=-1-2m=-1,1+2m<-1-2m三种情况求解不等式
(2)求出p:-2≤x≤10,q:-1-2m≤x≤-1+2m,由?p是?q的必要不充分条件,得q是p的必要不充分条件.即$\left\{{\begin{array}{l}{-1-2m≤-2}\\{-1+2m≥10}\\{m>0}\end{array}}\right.$,且等号不能同时取,
解得实数m的取值范围,
解答 解:(1)x2+2x+1-4m2=(x+1-2m)(x+1+2m)=0,
所以x2+2x+1-4m2=0对应的两根为-1+2m,-1-2m,
当m>0时,-1+2m>-1-2m,不等式的解集为{x|-1-2m≤x≤-1+2m},
当m=0时,-1+2m=-1-2m=-1,不等式的解集为{x|x=-1},
当m<0时,-1+2m<-1-2m,不等式的解集为{x|-1+2m≤x≤-1-2m};
(2)由-x2+8x+20≥0可得,(x-10)(x+2)≤0,
所以-2≤x≤10,即p:-2≤x≤10
由(1)知,当m>0时,不等式的解集为{x|-1-2m≤x≤-1+2m},
所以q:-1-2m≤x≤-1+2m,
∵?p是?q的必要不充分条件,∴q是p的必要不充分条件.
即$\left\{{\begin{array}{l}{-1-2m≤-2}\\{-1+2m≥10}\\{m>0}\end{array}}\right.$,且等号不能同时取,
解得$m≥\frac{11}{2}$.故实数m的取值范围为$m≥\frac{11}{2}$.
点评 本题考查了命题真假的应用,属于基础题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
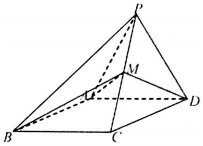 如图所示,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面ABCD是∠ABC=60°的菱形,M为PC的中点,PC=$\sqrt{6}$.
如图所示,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面ABCD是∠ABC=60°的菱形,M为PC的中点,PC=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [1,+∞) | C. | (1,+∞) | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com