练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．若函数f（x）=2ax2-x-1在（0，1）内恰有一个零点，则实数a的取值范围是（　　）
    A．（-1，1）B．[1，+∞）C．（1，+∞）D．（2，+∞）

    分析 讨论a的不同取值以确定方程是否是二次方程及二次方程的根的大致位置，再由方程的根与函数的零点的关系判断即可．

    解答 解：若函数f（x）=2ax2-x-1在区间（0，1）内恰有一个零点，
    则方程2ax2-x-1=0在区间（0，1）内恰有一个根，
    若a=0，则方程2ax2-x-1=0可化为：-x-1=0方程的解为-1，不成立；
    若a＜0，则方程2ax2-x-1=0不可能有正根，故不成立；
    若a＞0，则△=1+8a＞0，且c=-1＜0；
    故方程有一正一负两个根，
    故方程2ax2-x-1=0在区间（0，1）内恰有一个解可化为
    （2a•02-0-1）（2a•12-1-1）＜0；
    解得，a＞1；
    故实数a的取值范围是（1，+∞），
    故选：C．

    点评 本题考查了方程的根的判断及分类讨论的数学思想应用，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

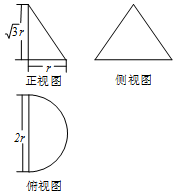    18．若一个空间几何体的三视图如图所示，且已知该几何体的体积为$\frac{\sqrt{3}}{6}π$，则其表面积为（　　）
    A．$\frac{3}{2}π+\sqrt{3}$B．$\frac{3}{2}π$C．$\frac{3}{4}π+2\sqrt{3}$D．$\frac{3}{4}π+\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

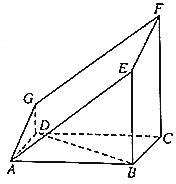    19．如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．
    （Ⅰ）求证：BD⊥平面ADG；
    （Ⅱ）求此多面体的全面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知命题p：-x2+8x+20≥0；命题q：x2+2x+1-4m2≤0．
    （1）当m∈R时，解不等式x2+2x+1-4m2≤0；
    （2）当m＞0时，若￢p是￢q的必要不充分条件，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．不等式$\frac{2-x}{x+1}$≥0的解集为（　　）
    A．{x|0＜x≤2}B．{x|-1＜x≤2}C．{x|x＞-1}D．R

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知球的半径为4，相互垂直的两个平面分别截球面得两个圆，若两圆的公共弦长为4，则两圆的圆心距等于（　　）
    A．2B．$2\sqrt{2}$C．$2\sqrt{3}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．执行如图所示的程序框图，则输出的结果是（　　）
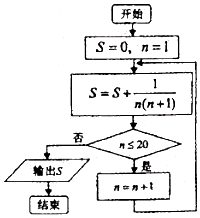
    A．$\frac{21}{22}$B．$\frac{20}{21}$C．$\frac{19}{20}$D．$\frac{22}{23}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设θ∈（0，$\frac{π}{2}$），且cos（θ+$\frac{π}{6}$）=$\frac{1}{3}$．
    （1）求sinθ的值；
    （2）求sin（2θ+$\frac{π}{6}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．下列函数中，为奇函数又在（0，+∞）上为减函数的是（　　）
    A．y=x-1B．y=sinxC．y=（$\frac{1}{2}$）xD．y=-|x|

    查看答案和解析>>

    同步练习册答案