
已知命题p:函数f(x)=lg(ax2﹣x+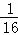 a)的定义域为R,命题q:q:不等式
a)的定义域为R,命题q:q:不等式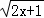 <1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( )
<1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( )
A. a>1 B. 1≤a≤2 C. a>2 D. 无解
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
如图13,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
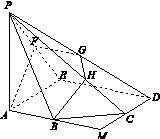
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
从集合{2,3,4,5}中随机抽取一个数a,从集合{1,3,5}中随机抽取一个数b,则向量m=(a,b)与向量n=(1,-1)垂直的概率为( )
A.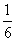 B.
B.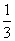
C.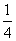 D.
D.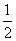
查看答案和解析>>
科目:高中数学 来源: 题型:
为了参加2014年青奥会高中篮球比赛,某中学决定从四个篮球较强的班级中选出12人组成男子篮球队代表所在地区参赛,队员来源人数如下表:
| 班级 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
| 人数 | 4 | 2 | 3 | 3 |
(1)从这12名队员中随机选出两名,求两人来自同一班级的概率;
(2)该中学篮球队经过奋力拼搏获得冠军.若要求选出两位队员代表冠军队发言,设其中来自高三(7)班的人数为ξ,求随机变量ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C:x2+2x+y2=0的一条斜率为1的切线为l1,且与l1垂直的直线l2平分该圆,则直线l2的方程为( )
A. x﹣y+1=0 B. x﹣y﹣1=0 C. x+y﹣1=0 D. x+y+1=0
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆T的中心为坐标原点O,右焦点为F(2,0),且椭圆T过点E(2,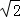 ).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
(1)求椭圆T的离心率;
(2)设△ABC的三条边所在直线的斜率分别为k1,k2,k3,且ki≠0,i=1,2,3.若直线OM,ON,OP的斜率之和为0,求证: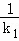 +
+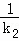 +
+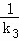 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图K42所示放置的边长为1的正三角形PAB沿x轴的负半轴按逆时针方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是____________________.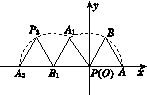
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com