
椭圆T的中心为坐标原点O,右焦点为F(2,0),且椭圆T过点E(2,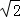 ).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
(1)求椭圆T的离心率;
(2)设△ABC的三条边所在直线的斜率分别为k1,k2,k3,且ki≠0,i=1,2,3.若直线OM,ON,OP的斜率之和为0,求证: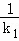 +
+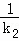 +
+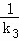 为定值.
为定值.
科目:高中数学 来源: 题型:
如图15,在四棱锥A BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .
.
(1)证明:DE⊥平面ACD;
(2)求二面角B AD E的大小.
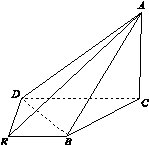
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,其分布列为P(X),则P(X=4)的值为( )
A.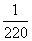 B.
B.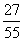
C.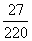 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:函数f(x)=lg(ax2﹣x+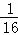 a)的定义域为R,命题q:q:不等式
a)的定义域为R,命题q:q:不等式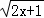 <1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( )
<1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( )
A. a>1 B. 1≤a≤2 C. a>2 D. 无解
查看答案和解析>>
科目:高中数学 来源: 题型:
过圆x2+y2﹣4x=0外一点P(m,n)作圆的两条切线,当这两条切线互相垂直时,m,n 应满足的关系式为( )
A. (m﹣2)2+n2=4 B. (m+2)2+n2=4 C. (m﹣2)2+n2=8 D. (m+2)2+n2=8
查看答案和解析>>
科目:高中数学 来源: 题型:
已知x,y为正实数,则( )
A. 2lgx+lgy=2lgx+2lgy B. 2lg(x+y)=2lgx·2lgy
C. 2lgx·lgy=2lgx+2lgy D. 2lg(xy)=2lgx·2lgy
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com