
已知平面内一点P∈{(x,y)|(x﹣2cosα)2+(y﹣2sinα)2=16,α∈R},则满足条件的点P在平面内所组成的图形的面积是 .
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
如图15,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
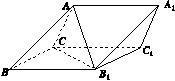
图15
(1)证明:AC=AB1;
(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A A1B1 C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按150进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失)得到的频率分布表如下:
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 合计 |
| 频数 |
|
|
| b | ||
| 频率 | a | 0.25 |
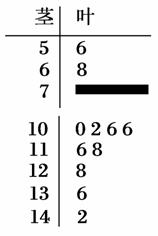
(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩及格率(分数在[90,150]范围为及格).
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C:x2+2x+y2=0的一条斜率为1的切线为l1,且与l1垂直的直线l2平分该圆,则直线l2的方程为( )
A. x﹣y+1=0 B. x﹣y﹣1=0 C. x+y﹣1=0 D. x+y+1=0
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆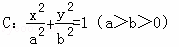 的左右焦点分别为F1,F2,若椭圆C上恰好有6个不同的点P,使得△F1F2P为等腰三角形,则椭圆C的离心率的取值范围是( )
的左右焦点分别为F1,F2,若椭圆C上恰好有6个不同的点P,使得△F1F2P为等腰三角形,则椭圆C的离心率的取值范围是( )
A. 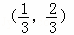 B.
B. 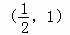 C.
C. 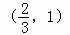 D.
D. 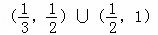
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆T的中心为坐标原点O,右焦点为F(2,0),且椭圆T过点E(2,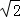 ).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
(1)求椭圆T的离心率;
(2)设△ABC的三条边所在直线的斜率分别为k1,k2,k3,且ki≠0,i=1,2,3.若直线OM,ON,OP的斜率之和为0,求证: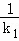 +
+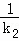 +
+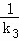 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列古典概型的说法中正确的个数是( )
①试验中所有可能出现的基本事件只有有限个;
②每个事件出现的可能性相等;
③基本事件的总数为n,随机事件A包含k个基本事件,则P(A)=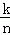 ;
;
④每个基本事件出现的可能性相等.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com