
如图15,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
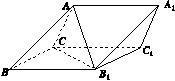
图15
(1)证明:AC=AB1;
(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A A1B1 C1的余弦值.
解:(1)证明:连接BC1,交B1C于点O,连接AO,因为侧面BB1C1C为菱形,所以B1C⊥BC1,且O为B1C及BC1的中点.
又AB⊥B1C,所以B1C⊥平面ABO.
由于AO⊂平面ABO,故B1C⊥AO.
又B1O=CO,故AC=AB1.
(2)因为AC⊥AB1,且O为B1C的中点,所以AO=CO.
又因为AB=BC,所以△BOA≌ △BOC.故OA⊥OB,从而OA,OB,OB1两两垂直.
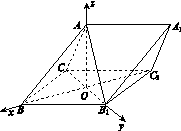
以O为坐标原点,OB的方向为x轴正方向,|OB|为单位长,建立如图所示的空间直角坐标系O xyz.
 所以可取n=(1,
所以可取n=(1, ,
, ).
).
设m是平面A1B1C1的法向量,
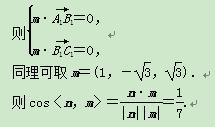 所以结合图形知二面角A A1B1 C1的余弦值为
所以结合图形知二面角A A1B1 C1的余弦值为 .
.


科目:高中数学 来源: 题型:
三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A NP M的余弦值.
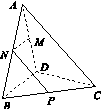
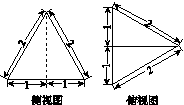
图14
查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( )
A.(-1,1,0) B.(1,-1,0)
C.(0,-1,1) D.(-1,0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图16所示,四棱柱ABCD A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1OB1D的余弦值.
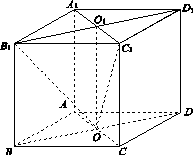
图16
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,在四棱锥A BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .
.
(1)证明:DE⊥平面ACD;
(2)求二面角B AD E的大小.
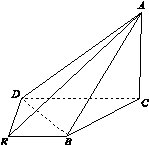
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图X261所示,在正方体ABCD A1B1C1D1中,M,N分别是棱C1D1,C1C的中点.给出以下四个结论:
①直线AM与直线C1C相交;
②直线AM与直线BN平行;
③直线AM与直线DD1异面;
④直线BN与直线MB1异面.
其中正确结论的序号为________(填入所有正确结论的序号).
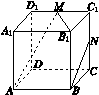
图X261
查看答案和解析>>
科目:高中数学 来源: 题型:
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:

(1)若视力测试结果不低于5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(2)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“好视力”学生的人数,求ξ的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com