
已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( )
A.(-1,1,0) B.(1,-1,0)
C.(0,-1,1) D.(-1,0,1)
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
设不等式组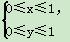 表示的平面区域为D,在D内任取一点P(x,y),若满足2x+y≤b的概率大于
表示的平面区域为D,在D内任取一点P(x,y),若满足2x+y≤b的概率大于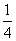 ,则实数b的取值范围是( )
,则实数b的取值范围是( )
A.(0,1) B.(0,2)
C.(1,+∞) D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图11,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
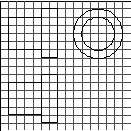
图11
A. B.
B.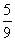 C.
C.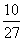 D.
D.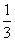
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
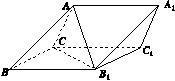
图15
(1)证明:AC=AB1;
(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A A1B1 C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图16,四棱锥P ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
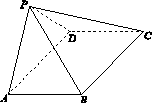
图16
(1)求证:AB⊥PD.
(2)若∠BPC=90°,PB= ,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
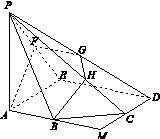
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.

图15
(1)证明:AC=AB1;
(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A A1B1 C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
一个坛子里有编号为1,2,…,12的12个大小相同的球,其中1到6号球是红球,其余的是黑球,若从中任取两个球,则取到的都是红球,且至少有1个球的号码是偶数的概率为( )
A.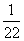 B.
B.
C.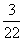 D.
D.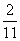
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C:x2+2x+y2=0的一条斜率为1的切线为l1,且与l1垂直的直线l2平分该圆,则直线l2的方程为( )
A. x﹣y+1=0 B. x﹣y﹣1=0 C. x+y﹣1=0 D. x+y+1=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com