
如图13,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
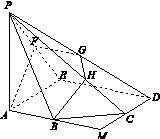
图13
科目:高中数学 来源: 题型:
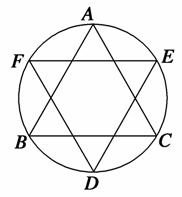
如图,△ABC和△DEF都是圆内接正三角形,且BC∥EF.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在△ABC内”,B表示事件“豆子落在△DEF内”,则P(B|A)=( )
A.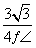 B.
B.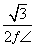
C.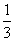 D.
D.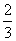
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
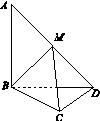
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
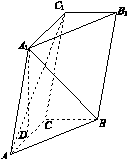
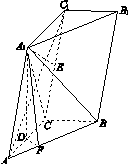
如图11所示,三棱柱ABC A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为 ,求二面角A1 AB C的大小.
,求二面角A1 AB C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( )
A.(-1,1,0) B.(1,-1,0)
C.(0,-1,1) D.(-1,0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二面角αlβ为60°,AB⊂α,AB⊥l,A为垂足,CD⊂β,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )
A.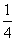 B.
B.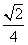
C.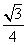 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,在四棱锥A BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .
.
(1)证明:DE⊥平面ACD;
(2)求二面角B AD E的大小.
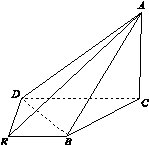
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙、丙3位教师安排在周一至周五中的3天值班,要求每人值班1天且每天至多安排1人,则恰好甲安排在另外两位教师前面值班的概率是( )
A.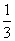 B.
B. C.
C.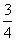 D.
D.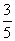
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:函数f(x)=lg(ax2﹣x+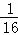 a)的定义域为R,命题q:q:不等式
a)的定义域为R,命题q:q:不等式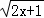 <1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( )
<1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( )
A. a>1 B. 1≤a≤2 C. a>2 D. 无解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com