
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
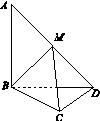
图15
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
已知盒子中有散落的棋子15粒,其中6粒是黑子,9粒是白子,已知从中取出2粒都是黑子的概率是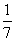 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是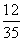 ,现从中任意取出2粒恰好是同色的概率是________.
,现从中任意取出2粒恰好是同色的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在一块耕地上种植一种作物,每季种植成本为1 000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
| 作物产量(kg) | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| 作物市场价格(元/kg) | 6 | 10 |
| 概率 | 0.4 | 0.6 |
(1)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2 000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图11,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
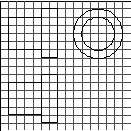
图11
A. B.
B.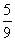 C.
C.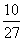 D.
D.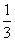
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设二面角DAEC为60°,AP=1,AD= ,求三棱锥EACD的体积.
,求三棱锥EACD的体积.
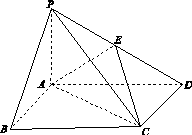
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,三棱柱ABC A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
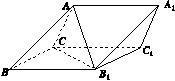
图15
(1)证明:AC=AB1;
(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A A1B1 C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
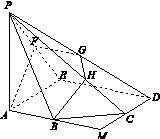
图13
查看答案和解析>>
科目:高中数学 来源: 题型:
从集合{2,3,4,5}中随机抽取一个数a,从集合{1,3,5}中随机抽取一个数b,则向量m=(a,b)与向量n=(1,-1)垂直的概率为( )
A.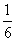 B.
B.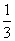
C.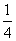 D.
D.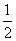
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com