
在一块耕地上种植一种作物,每季种植成本为1 000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
| 作物产量(kg) | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| 作物市场价格(元/kg) | 6 | 10 |
| 概率 | 0.4 | 0.6 |
(1)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2 000元的概率.
解 (1)设A表示事件“作物产量为300 kg”,B表示事件“作物市场价格为6元/kg”,
由题设知P(A)=0.5,P(B)=0.4,
∵利润=产量×市场价格-成本,
∴X所有可能的取值为
500×10-1 000=4 000,500×6-1 000=2 000,
300×10-1 000=2 000,300×6-1 000=800.
P(X=4 000)=P(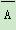 )P(
)P(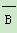 )=(1-0.5)×(1-0.4)=0.3,
)=(1-0.5)×(1-0.4)=0.3,
P(X=2 000)=P(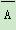 )P(B)+P(A)P(
)P(B)+P(A)P(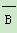 )=(1-0.5)×0.4+0.5×(1-0.4)=0.5,
)=(1-0.5)×0.4+0.5×(1-0.4)=0.5,
P(X=800)=P(A)P(B)=0.5×0.4=0.2,
所以X的分布列为
| X | 4 000 | 2 000 | 800 |
| P | 0.3 | 0.5 | 0.2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
航天员拟在太空授课,准备进行标号为0,1,2,3,4,5的六项实验,向全世界人民普及太空知识,其中0号实验不能放在第一项,最后一项的标号小于它前面相邻一项的标号,则实验顺序的编排方法种数为________.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
在长为12 cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积小于32 cm2的概率为( )
A.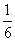 B.
B.
C.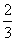 D.
D.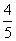
查看答案和解析>>
科目:高中数学 来源: 题型:
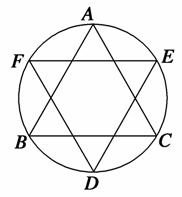
如图,△ABC和△DEF都是圆内接正三角形,且BC∥EF.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在△ABC内”,B表示事件“豆子落在△DEF内”,则P(B|A)=( )
A.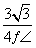 B.
B.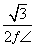
C.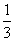 D.
D.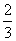
查看答案和解析>>
科目:高中数学 来源: 题型:
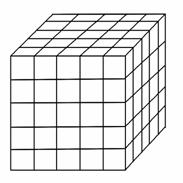
.如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体.经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )
A.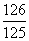 B.
B.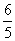
C.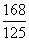 D.
D.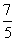
查看答案和解析>>
科目:高中数学 来源: 题型:
低碳生活,从“衣食住行”开始.在国内一些网站中出现了“碳足迹”的应用,人们可以由此计算出自己每天的碳排放量,如家居用电的二氧化碳排放量(kg)=耗电度数×0.785,家用天然气的二氧化碳排放量(kg)=天然气使用立方数×0.19等.某校开展“节能减排,保护环境,从我做起!”的活动,该校高一(六)班同学利用假期在东城、西城两个小区进行了逐户的关于“生活习惯是否符合低碳排放标准”的调查.生活习惯符合低碳观念的称为“低碳家庭”,否则称为“非低碳家庭”.经统计,这两类家庭占各自小区总户数的比例P数据如下:
| 东城小区 | 低碳家庭 | 非低碳家庭 |
| 比例P |
|
|
| 西城小区 | 低碳家庭 | 非低碳家庭 |
| 比例P |
|
|
(1)如果在东城、西城两个小区内各随机选择2个家庭,求这4个家庭中恰好有两个家庭是“低碳家庭”的概率;
(2)该班同学在东城小区经过大力宣传节能减排的重要意义,每周“非低碳家庭”中有20%的家庭能加入到“低碳家庭”的行列中.宣传两周后随机地从东城小区中任选5个家庭,记ξ表示5个家庭中“低碳家庭”的个数,求E(ξ)和D(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
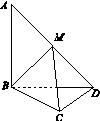
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
如图15,在四棱锥A BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .
.
(1)证明:DE⊥平面ACD;
(2)求二面角B AD E的大小.
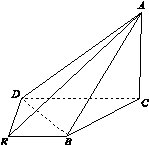
图15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com